��Ŀ����
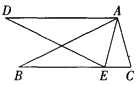
����Ŀ��������y=�� ![]() ��x��1��2+3��y�ύ�ڵ�A������ΪB���Գ���BC��x�ύ�ڵ�C��
��x��1��2+3��y�ύ�ڵ�A������ΪB���Գ���BC��x�ύ�ڵ�C��
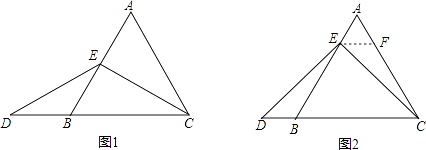
��1����ͼ1�����A�����꼰�߶�OC�ij���
��2����P���������ϣ�ֱ��PQ��BC��x���ڵ�Q������BQ��
������45��ǵ�ֱ�����ǰ���ͼ2��ʾ���ã����У�һ���������C�غϣ�ֱ�Ƕ���D��BQ�ϣ���һ������E��PQ�ϣ���ֱ��BQ�ĺ�������ʽ��
������30��ǵ�ֱ�����ǰ�һ���������C�غϣ�ֱ�Ƕ���D��ֱ��BQ�ϣ���һ������E��PQ�ϣ����P�����꣮
���𰸡�
��1��
�⣺��x=0���������ߵã�y= ![]() ��
��
���A��0�� ![]() ����
����
�����ߵĶԳ���Ϊx=1��
��OC=1
��2��
�⣺����ͼ��B��1��3��
�ֱ����D��DM��x����M��DN��PQ�ڵ�N��
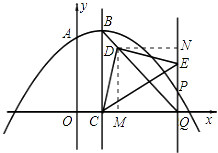
��PQ��BC��
���DMQ=��DNQ=��MQN=90�㣬
���ı���DMQN�Ǿ��Σ�
�ߡ�CDE�ǵ���ֱ�������Σ�
��DC=DE����CDM=��EDN
�� 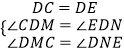 ��
��
���CDM�ա�EDN��AAS��
��DM=DN��
�����DMQN��������
���BQC=45��
��CQ=CB=3
��Q��4��0��
��BQ�Ľ���ʽΪ��y=kx+b��
��B��1��3����Q��4��0���������ʽ�ã�k=��1��b=4��
����ֱ��BQ�Ľ���ʽΪ��y=��x+4��
�ڵ���P�ڶԳ����Ҳ࣬��ͼ��
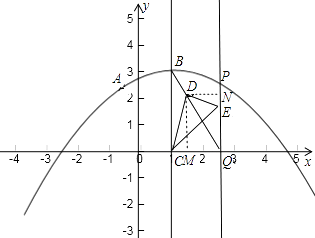
����D��DM��x����M��DN��PQ��N��
�ߡ�CDE=90�㣬���CDM=��EDN
���CDM�ס�EDN
����DCE=30�㣬 ![]() =
= ![]()
��DN=MQ
�� ![]() =
= ![]()
�� ![]() =
= ![]() ��BC=3��CQ=
��BC=3��CQ= ![]()
��Q��1+ ![]() ��0��
��0��
��P1��1+ ![]() ��
�� ![]() ��
��
����DCE=60�㣬��P2��1+3 ![]() ����
���� ![]() ����
����
����P�ڶԳ�������ʱ���ɶԳ���֪��
P3��1�� ![]() ��
�� ![]() ����P4��1��3
����P4��1��3 ![]() ����
���� ![]() ��
��
����������P1��1+ ![]() ��
�� ![]() ����P2��1+3
����P2��1+3 ![]() ����
���� ![]() ����P3��1��
����P3��1�� ![]() ��
�� ![]() ����P4��1��3
����P4��1��3 ![]() ����
���� ![]() ����
����
����������1����x=0�������������y��ֵȷ����A�����꣬��������ߵĶԳ���õ�OC�ij�����2�����ɡ�CDE�ǵ���ֱ�������Σ��ֱ����D��x���PQ�Ĵ��ߣ�ͨ��������ȫ�ȵõ���DQO=45�㣬�����Q�����꣬Ȼ���ô���ϵ�������BQ�Ľ���ʽ���ڷֵ�P�ڶԳ���������������ۣ����������������������Q�����꣬Ȼ����������������P�����꣮

����Ŀ��ij�о���֪ʶ������AУ��BУ���ɳ�5��ѡ����ɴ����ӲμӾ�������У�ɳ�ѡ�ֵľ����ɼ���ͼ��ʾ��
(1)����ͼʾ��д�±���
ƽ����/�� | ��λ��/�� | ����/�� | |
AУ | ______ | 85 | ______ |
BУ | 85 | ______ | 100 |
(2)�����У�ɼ���ƽ��������λ���������ĸ�ѧУ�ľ����ɼ��Ϻã�
(3)������У�����ɼ��ķ�����ж��ĸ�ѧУ������ѡ�ֳɼ���Ϊ�ȶ���