题目内容
已知关于 的一元二次方程
的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求 的取值范围;
的取值范围;
(2)若 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求 的值.
的值.
【答案】
(1)k< ;(2)k=2.
;(2)k=2.
【解析】
试题分析:(1)一元二次方程的解的情况与它的判别式 =b2-4ac的符号有关,当
=b2-4ac的符号有关,当 >0时,一元二次方程有两个不相等的实数根,当
>0时,一元二次方程有两个不相等的实数根,当 <0时,一元二次方程没有实数根,当
<0时,一元二次方程没有实数根,当 =0时,一元二次方程有两个相等的实数根.据此可求出k的取值范围.(2)由于k为正整数,又有(1)可知k<
=0时,一元二次方程有两个相等的实数根.据此可求出k的取值范围.(2)由于k为正整数,又有(1)可知k< ,所以k=1或2,分别代入方程中,求得方程的解,能使方程的根都是整数的k的值就是所要求的值.
,所以k=1或2,分别代入方程中,求得方程的解,能使方程的根都是整数的k的值就是所要求的值.
试题解析:解:(1)△=4-4(2k-4)=20-8k
∵方程有两个不相等的实根
∴△>0即20-8k>0 ∴k< 3分
3分
(2)∵k为正整数,且k< ,∴k=1或2,
,∴k=1或2,
∵方程的根x= 为整数
∴5-2k为完全平方数
为整数
∴5-2k为完全平方数
当k=1时,5-2k=3,不合题意;当k=2时,5-2k=1 ∴k=2 7分
考点:1、一元二次方程根的判别式;2、解方程.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
. 的取值范围;
的取值范围; 时,求
时,求 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
. 的取值范围;
的取值范围;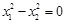 时,求
时,求 的一元二次方程
的一元二次方程 有两个实数根,求
有两个实数根,求 的取值范围及
的取值范围及 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
. 的取值范围;
的取值范围; 时,求
时,求 的一元二次方程
的一元二次方程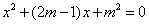 有两个实数根
有两个实数根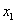 和
和 .
. 的取值范围;
的取值范围; 时,求
时,求