题目内容
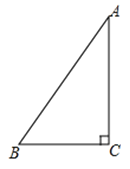
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)请用直尺和圆规按下列步骤作图,保留作图痕迹:
①作∠ACB的平分线,交斜边AB于点D;
②过点D作AC的垂线,垂足为点E.
(2)在(1)作出的图形中,若CB=6,DE=4,则△BCD的面积为 .
【答案】(1)作图见解析;(2)12
【解析】分析:
(1)以C为圆心,任意长为半径画弧,交BC,AC两点,再以这两点为圆心,大于这两点的线段的一半为半径画弧,过这两弧的交点与C在直线交AB于D即可,根据过直线外一点作已知直线的垂线的方法可作出垂线即可;
(2)根据平行线的性质和角平分线的性质推出∠ECD=∠EDC,进而证得DE=CE,结合三角形的面积公式进行解答.
本题解析:
(1)如图所示:
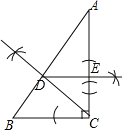
(2)∵DC是∠ACB的平分线,
∴∠BCD=∠ACD,
∵DE⊥AC,BC⊥AC,
∴DE∥BC,
∴∠EDC=∠BCD,
∴∠ECD=∠EDC,
∴DE=CE=4,
∴S△BCD=![]() BCCE=
BCCE=![]() ×6×4=12.
×6×4=12.
故答案是:12.

练习册系列答案
相关题目