题目内容
高速公路BC(公路视为直线)的最高限速为120千米/时(即| 100 |
| 3 |
(1)求点B与点C的距离;
(2)测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是2.5秒,试通
 过计算,判断该汽车在这段限速路上是否超速?(参考数据:
过计算,判断该汽车在这段限速路上是否超速?(参考数据:| 3 |
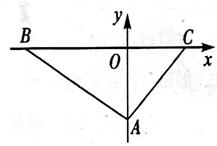
分析:(1)构造30°的三角形所在的直角三角形,由AH为20米,利用点A到点B的距离与点A离地面的距离之比为13:5,可得BH长;利用30°正切值可求得CH长,让它们相加即可;
(2)利用速度=路程÷时间求得速度,和最高限速比较即可.
(2)利用速度=路程÷时间求得速度,和最高限速比较即可.
解答: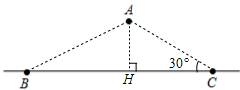 解:(1)在Rt△AHB中,
解:(1)在Rt△AHB中,
∵AB:AH=13:5,
∴BH:AH=12:5,
∵AH=20,
∴BH=48,
在Rt△AHC中,∵∠ACH=30°,
∴CH=AH•cot30°=20
,
BC=(48+20
)米,
∴点B与点C的距离为(48+20
)千米;
(2)∵BC=48+20
,
∴
≈32.8,
∵32.8<
,
∴这辆汽车没超速.
 解:(1)在Rt△AHB中,
解:(1)在Rt△AHB中,∵AB:AH=13:5,
∴BH:AH=12:5,
∵AH=20,
∴BH=48,
在Rt△AHC中,∵∠ACH=30°,
∴CH=AH•cot30°=20
| 3 |
BC=(48+20
| 3 |
∴点B与点C的距离为(48+20
| 3 |
(2)∵BC=48+20
| 3 |
∴
48+20
| ||
| 2.5 |
∵32.8<
| 100 |
| 3 |
∴这辆汽车没超速.
点评:考查仰角的定义,能借助仰角构造直角三角形并解直角三角形是仰角问题常用的方法.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
 米/秒).在该公路正上方离地面20米的点A处设置了一个测速仪(如图所示).已知点A到点B的距离与点A离地面的距离之比为13:5,点A测得点C的俯角为30°.
米/秒).在该公路正上方离地面20米的点A处设置了一个测速仪(如图所示).已知点A到点B的距离与点A离地面的距离之比为13:5,点A测得点C的俯角为30°. 过计算,判断该汽车在这段限速路上是否超速?(参考数据:
过计算,判断该汽车在这段限速路上是否超速?(参考数据: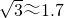 )
)
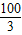 米/秒).在该公路正上方离地面20米的点A处设置了一个测速仪(如图所示).已知点A到点B的距离与点A离地面的距离之比为13:5,点A测得点C的俯角为30°.
米/秒).在该公路正上方离地面20米的点A处设置了一个测速仪(如图所示).已知点A到点B的距离与点A离地面的距离之比为13:5,点A测得点C的俯角为30°.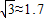 )
)
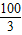 米/秒).在该公路正上方离地面20米的点A处设置了一个测速仪(如图所示).已知点A到点B的距离与点A离地面的距离之比为13:5,点A测得点C的俯角为30°.
米/秒).在该公路正上方离地面20米的点A处设置了一个测速仪(如图所示).已知点A到点B的距离与点A离地面的距离之比为13:5,点A测得点C的俯角为30°. )
)