题目内容
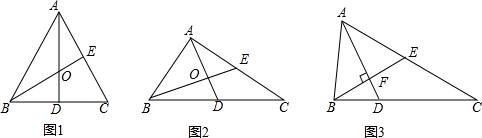
(2012•房山区二模)如图1,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)如图2,若∠AED=2∠EAD,AC=6.求DE的长.
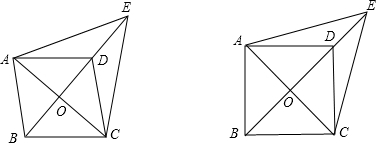
(1)求证:四边形ABCD是菱形;
(2)如图2,若∠AED=2∠EAD,AC=6.求DE的长.

分析:(1)根据对角线互相垂直的平行四边形是菱形.由四边形ABCD是平行四边形,可得AO=CO.又由△ACE是等边三角形,可得AE=CE.根据三线合一,对角线垂直,即可得四边形既为菱形;
(2)根据有一个角是90°的菱形是正方形.由题意易得∠BAO=∠EAO-∠EAB=60°-15°=45°,即四边形ABCD是正方形,利用正方形的性和等边三角形的性质即可求出DE的长.
(2)根据有一个角是90°的菱形是正方形.由题意易得∠BAO=∠EAO-∠EAB=60°-15°=45°,即四边形ABCD是正方形,利用正方形的性和等边三角形的性质即可求出DE的长.
解答:证明:(1)∵四边形ABCD是平行四边形
∴OA=OC,
∵△ACE是等边三角形.
∴OE⊥AC,
∴BD⊥AC,
∴四边形ABCD是菱形;
(2)∵△ACE是等边三角形,OE⊥AC,
∴∠AEO=
∠AEC=30°,
∵∠AED=2∠EAD,
∴∠EAD=15°
∴∠ADB=45°,
∵四边形ABCD是菱形,
∴AD=DC,BD⊥AC,
∴∠CDB=∠ADB=45°
∴∠ADC=90°,
∴△ADC是等腰直角三角形,
∴OA=OC=OD=
AC=3,
∵△ACE是等边三角形,
∴∠EAO=60°
在Rt△AOE中,OE=OAtan60°=3
∴DE=OE-OD=3
-3.
∴OA=OC,
∵△ACE是等边三角形.
∴OE⊥AC,
∴BD⊥AC,
∴四边形ABCD是菱形;
(2)∵△ACE是等边三角形,OE⊥AC,
∴∠AEO=
| 1 |
| 2 |
∵∠AED=2∠EAD,
∴∠EAD=15°
∴∠ADB=45°,
∵四边形ABCD是菱形,
∴AD=DC,BD⊥AC,
∴∠CDB=∠ADB=45°
∴∠ADC=90°,
∴△ADC是等腰直角三角形,
∴OA=OC=OD=
| 1 |
| 2 |
∵△ACE是等边三角形,
∴∠EAO=60°
在Rt△AOE中,OE=OAtan60°=3
| 3 |
∴DE=OE-OD=3
| 3 |
点评:此题主要考查菱形和正方形的判定.本题考查知识点较多,综合性强,能力要求全面,难度中等.注意灵活运用正方形和菱形的判定方法.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
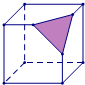 (2012•房山区二模)过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其正确展开图为( )
(2012•房山区二模)过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其正确展开图为( )