题目内容
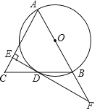
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 与
与![]() 边交于点
边交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OD,根据等边对等角得到∠A=∠ADO,再结合平行线的性质可得到∠DOE=∠COE,从而得到△ODE≌△OCE,根据全等三角形的性质得到∠ODE=∠ACB=90°,由此得到结论;
(2)连接CD,根据平行线等分线段定理得到BE=CE,根据勾股定理得到AB=10,由三角形的面积公式得到CD的长.在Rt△CBD中,由勾股定理即可得到结论.
(1)连接OD.
∵OA=OD,∴∠A=∠ADO.
∵OE∥AB,∴∠A=∠EOC,∠ADO=∠DOE,∴∠DOE=∠COE.
在△ODE与△OCE中,∵OD=OC,∠DOE=∠COE,OE=OE,∴△ODE≌△OCE,∴∠ODE=∠ACB=90°,∴DE是⊙O的切线;
(2)连接CD.
∵OE∥AB,AO=OC,∴BE=EC.
∵⊙O的半径为3,EC=4,∴BC=8,AC=6.
∵∠ACB=90°,∴AB=10.
∵AC是直径,∴∠ADC=90°.
∵S△ABC=![]() ACBC=
ACBC=![]() ABCD,∴6×8=10×CD,解得:CD=
ABCD,∴6×8=10×CD,解得:CD=![]() ,∴BD=
,∴BD=![]() =
=![]() .
.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目