ĢāÄæÄŚČŻ
 ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÄŚ£¬¶ž“ĪŗÆŹży=ax2+bx+cĶ¼ĻóÓėxÖį½»ÓŚA£Ø-1£¬0£©£¬B£Ø4£¬0£©Į½µć£¬ÓėyÖį½»ÓŚµćC£Ø0£¬4£©£¬Ö±Ļßy=x+1Óė¶ž“ĪŗÆŹżµÄĶ¼Ļó½»ÓŚA”¢DĮ½µć£¬
ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÄŚ£¬¶ž“ĪŗÆŹży=ax2+bx+cĶ¼ĻóÓėxÖį½»ÓŚA£Ø-1£¬0£©£¬B£Ø4£¬0£©Į½µć£¬ÓėyÖį½»ÓŚµćC£Ø0£¬4£©£¬Ö±Ļßy=x+1Óė¶ž“ĪŗÆŹżµÄĶ¼Ļó½»ÓŚA”¢DĮ½µć£¬£Ø1£©Ēó³ö¶ž“ĪŗÆŹżµÄ½āĪöŹ½ŅŌ¼°DµćµÄ×ų±ź£»
£Ø2£©µćPŹĒÖ±ĻßADÉĻ·½Å×ĪļĻßÉĻµÄŅ»µć£¬Į¬½įPB£¬½»ADÓŚµćE£¬Ź¹
| PE |
| BE |
| 4 |
| 5 |
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Į¬½įPD£¬
¢ŁÖ±½ÓŠ“³öPDÓėADµÄ¹ŲĻµ
PD”ĶAD
PD”ĶAD
£»¢ŚµćMŹĒĘ½ĆęÄŚŅ»µć£¬Ź¹”÷PDM”×”÷ADB£¬Ēó·ūŗĻŅŖĒóµÄĖłÓŠµćMµÄ×ų±ź£®
·ÖĪö£ŗ£Ø1£©°ŃµćA”¢B”¢CµÄ×ų±ź“śČė¶ž“ĪŗÆŹż½āĪöŹ½£¬ĄūÓĆ“ż¶ØĻµŹż·ØĒóŗÆŹż½āĪöŹ½½ā“š£¬ŌŁÓėÖ±Ļßy=x+1ĮŖĮ¢Ēó½ā¼“æɵƵ½µćDµÄ×ų±ź£»
£Ø2£©ÉčPF”ĪAD½»xÖįÓŚF£¬øł¾ŻĘ½ŠŠĻß·ÖĻ߶Ī³É±ČĄż¶ØĄķĒó³öAFµÄ³¤¶Č£¬ŌŁĒó³öÖ±ĻßPFµÄ½āĪöŹ½£¬Č»ŗóÓė¶ž“ĪŗÆŹż½āĪöŹ½ĮŖĮ¢Ēó½ā¼“æɵƵ½µćPµÄ×ų±ź£»
£Ø3£©¢ŁÉčÖ±ĻßPDµÄ½āĪöŹ½ĪŖy=kx+b£¬ĄūÓĆ“ż¶ØĻµŹż·ØĒó³öÖ±ĻߵĽāĪöŹ½£¬“Ó¶ųµĆµ½Ö±ĻßPDÓėxÖįµÄ¼Š½ĒĪŖ45”ć£¬ÅŠ¶ØPDÓėAD“¹Ö±£»
¢ŚĄūÓĆ¹“¹É¶ØĄķĮŠŹ½Ēó³öAD£¬øł¾ŻµćP”¢DµÄ×ų±źĒó³öPDµÄ³¤¶Č£¬Č»ŗóøł¾ŻÖ±ĻßPDÓėxÖįµÄ¼Š½ĒĪŖ45”ć£¬ĄūÓĆĻąĖĘČż½ĒŠĪ¶ŌÓ¦±ß³É±ČĄżĮŠŹ½Ēó³öPMµÄ³¤¶Č£¬·Ö¢ŁµćMŌŚPDĻĀ·½Ź±£¬PM”ĪyÖį£¬Ēó³öµćMµÄׯ×ų±ź£¬“Ó¶ųµĆ½ā£»¢ŚµćMŌŚPDÉĻ·½Ź±£¬PM”ĪxÖį£¬Ēó³öµćMµÄŗį×ų±ź£¬“Ó¶ųµĆ½ā£®
£Ø2£©ÉčPF”ĪAD½»xÖįÓŚF£¬øł¾ŻĘ½ŠŠĻß·ÖĻ߶Ī³É±ČĄż¶ØĄķĒó³öAFµÄ³¤¶Č£¬ŌŁĒó³öÖ±ĻßPFµÄ½āĪöŹ½£¬Č»ŗóÓė¶ž“ĪŗÆŹż½āĪöŹ½ĮŖĮ¢Ēó½ā¼“æɵƵ½µćPµÄ×ų±ź£»
£Ø3£©¢ŁÉčÖ±ĻßPDµÄ½āĪöŹ½ĪŖy=kx+b£¬ĄūÓĆ“ż¶ØĻµŹż·ØĒó³öÖ±ĻߵĽāĪöŹ½£¬“Ó¶ųµĆµ½Ö±ĻßPDÓėxÖįµÄ¼Š½ĒĪŖ45”ć£¬ÅŠ¶ØPDÓėAD“¹Ö±£»
¢ŚĄūÓĆ¹“¹É¶ØĄķĮŠŹ½Ēó³öAD£¬øł¾ŻµćP”¢DµÄ×ų±źĒó³öPDµÄ³¤¶Č£¬Č»ŗóøł¾ŻÖ±ĻßPDÓėxÖįµÄ¼Š½ĒĪŖ45”ć£¬ĄūÓĆĻąĖĘČż½ĒŠĪ¶ŌÓ¦±ß³É±ČĄżĮŠŹ½Ēó³öPMµÄ³¤¶Č£¬·Ö¢ŁµćMŌŚPDĻĀ·½Ź±£¬PM”ĪyÖį£¬Ēó³öµćMµÄׯ×ų±ź£¬“Ó¶ųµĆ½ā£»¢ŚµćMŌŚPDÉĻ·½Ź±£¬PM”ĪxÖį£¬Ēó³öµćMµÄŗį×ų±ź£¬“Ó¶ųµĆ½ā£®
½ā“š£ŗ½ā£ŗ£Ø1£©”߶ž“ĪŗÆŹży=ax2+bx+cĶ¼Ļó¾¹żA£Ø-1£¬0£©£¬B£Ø4£¬0£©£¬C£Ø0£¬4£©£¬
”ą
£¬
½āµĆ
£¬
ĖłŅŌ£¬¶ž“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy=-x2+3x+4£¬
ĮŖĮ¢
£¬
½āµĆ
£ØĪŖµćA×ų±ź£©£¬
£¬
ĖłŅŌ£¬µćDµÄ×ų±źĪŖ£Ø3£¬4£©£»
£Ø2£©ÉčPF”ĪAD½»xÖįÓŚF£¬
Ōņ
=
£¬
”ßA£Ø-1£¬0£©£¬B£Ø4£¬0£©£¬
”ąAB=4-£Ø-1£©=5£¬
”ą
=
£¬
½āµĆAF=4£¬
”ąOF=4+1=5£¬
µćFµÄ×ų±źĪŖ£Ø-5£¬0£©£¬
Ņ×ĒóÖ±ĻßPFµÄ½āĪöŹ½ĪŖy=x+5£¬
ĮŖĮ¢
£¬
½āµĆ
£¬
ĖłŅŌ£¬µćPµÄ×ų±źĪŖ£Ø1£¬6£©£»
£Ø3£©¢ŁÉčÖ±ĻßPDµÄ½āĪöŹ½ĪŖy=kx+b£¬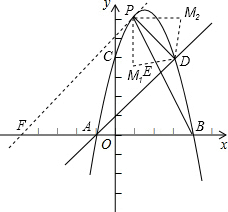
Ōņ
£¬
½āµĆ
£¬
ĖłŅŌ£¬Ö±ĻßPDµÄ½āĪöŹ½ĪŖy=-x+7£¬
”ąÖ±ĻßPDÓėxÖįµÄøŗ·½Ļņ¼Š½ĒĪŖ45”ć£¬
”ßÖ±Ļßy=x+1ÓėxÖįµÄÕż·½Ļņ¼Š½ĒĪŖ45”ć£¬
”ąPD”ĶAD£»
¢Śøł¾Ż¹“¹É¶ØĄķ£¬AD=
=4
£¬
”ßP£Ø1£¬6£©£¬D£Ø3£¬4£©£¬
”ąPD=
=2
£¬
”ß”ĻDAB=45”ć£¬PDÓėxÖįøŗ·½Ļņ¼Š½ĒĪŖ45”ć£¬
”ąPM”ĪyÖį»ņPM”ĪxÖį£¬
”ß”÷PDM”×”÷ADB£¬
”ą
=
£¬
¼“
=
£¬
½āµĆPM=
£¬
¢ŁµćMŌŚPDĻĀ·½Ź±£¬PM”ĪyÖį£¬µćMµÄׯ×ų±źĪŖ6-
=
£¬
“ĖŹ±£¬µćMµÄ×ų±źĪŖM1£Ø1£¬
£©£¬
¢ŚµćMŌŚPDÉĻ·½Ź±£¬PM”ĪxÖį£¬µćMµÄŗį×ų±źĪŖ1+
=
£¬
“ĖŹ±£¬µćMµÄ×ų±źĪŖM2£Ø
£¬6£©£¬
×ŪÉĻĖłŹö£¬µćMµÄ×ų±źĪŖ£Ø1£¬
£©»ņ£Ø
£¬6£©Ź±£¬”÷PDM”×”÷ADB£®
”ą
|
½āµĆ
|
ĖłŅŌ£¬¶ž“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy=-x2+3x+4£¬
ĮŖĮ¢
|
½āµĆ
|
|
ĖłŅŌ£¬µćDµÄ×ų±źĪŖ£Ø3£¬4£©£»
£Ø2£©ÉčPF”ĪAD½»xÖįÓŚF£¬
Ōņ
| AF |
| AB |
| PE |
| BE |
”ßA£Ø-1£¬0£©£¬B£Ø4£¬0£©£¬
”ąAB=4-£Ø-1£©=5£¬
”ą
| AF |
| 5 |
| 4 |
| 5 |
½āµĆAF=4£¬
”ąOF=4+1=5£¬
µćFµÄ×ų±źĪŖ£Ø-5£¬0£©£¬
Ņ×ĒóÖ±ĻßPFµÄ½āĪöŹ½ĪŖy=x+5£¬
ĮŖĮ¢
|
½āµĆ
|
ĖłŅŌ£¬µćPµÄ×ų±źĪŖ£Ø1£¬6£©£»
£Ø3£©¢ŁÉčÖ±ĻßPDµÄ½āĪöŹ½ĪŖy=kx+b£¬

Ōņ
|
½āµĆ
|
ĖłŅŌ£¬Ö±ĻßPDµÄ½āĪöŹ½ĪŖy=-x+7£¬
”ąÖ±ĻßPDÓėxÖįµÄøŗ·½Ļņ¼Š½ĒĪŖ45”ć£¬
”ßÖ±Ļßy=x+1ÓėxÖįµÄÕż·½Ļņ¼Š½ĒĪŖ45”ć£¬
”ąPD”ĶAD£»
¢Śøł¾Ż¹“¹É¶ØĄķ£¬AD=
| (3+1)2+42 |
| 2 |
”ßP£Ø1£¬6£©£¬D£Ø3£¬4£©£¬
”ąPD=
| (1-3)2+(6-4)2 |
| 2 |
”ß”ĻDAB=45”ć£¬PDÓėxÖįøŗ·½Ļņ¼Š½ĒĪŖ45”ć£¬
”ąPM”ĪyÖį»ņPM”ĪxÖį£¬
”ß”÷PDM”×”÷ADB£¬
”ą
| PM |
| AB |
| PD |
| AD |
¼“
| PM |
| 5 |
2
| ||
4
|
½āµĆPM=
| 5 |
| 2 |
¢ŁµćMŌŚPDĻĀ·½Ź±£¬PM”ĪyÖį£¬µćMµÄׯ×ų±źĪŖ6-
| 5 |
| 2 |
| 7 |
| 2 |
“ĖŹ±£¬µćMµÄ×ų±źĪŖM1£Ø1£¬
| 7 |
| 2 |
¢ŚµćMŌŚPDÉĻ·½Ź±£¬PM”ĪxÖį£¬µćMµÄŗį×ų±źĪŖ1+
| 5 |
| 2 |
| 7 |
| 2 |
“ĖŹ±£¬µćMµÄ×ų±źĪŖM2£Ø
| 7 |
| 2 |
×ŪÉĻĖłŹö£¬µćMµÄ×ų±źĪŖ£Ø1£¬
| 7 |
| 2 |
| 7 |
| 2 |
µćĘĄ£ŗ±¾ĢāŹĒ¶ž“ĪŗÆŹż×ŪŗĻĢāŠĶ£¬Ö÷ŅŖæ¼²éĮĖ“ż¶ØĻµŹż·ØĒ󶞓ĪŗÆŹż½āĪöŹ½£¬ĮŖĮ¢Į½ŗÆŹż½āĪöŹ½Ēó½»µć×ų±ź£¬Ę½ŠŠĻß·ÖĻ߶Ī³É±ČĄż¶ØĄķ£¬ĻąĖĘČż½ĒŠĪ¶ŌÓ¦±ß³É±ČĄżµÄŠŌÖŹ£¬Į½µć¼äµÄ¾ąĄė¹«Ź½£¬£Ø2£©æ¼ĀĒµ½ĄūÓĆPF”ĪAD£¬øł¾ŻĘ½ŠŠĻß·ÖĻ߶Ī³É±ČĄż¶ØĄķĒó³öÖ±ĻßPFµÄ½āĪöŹ½ŹĒ½āĢāµÄ¹Ų¼ü£¬£Ø3£©ÅŠ¶Ļ³öPM”ĪyÖį»ņPM”ĪxÖįŹĒ½āĢāµÄ¹Ų¼ü£®

Į·Ļ°²įĻµĮŠ“š°ø
 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
Ļą¹ŲĢāÄæ
 ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÄŚ£¬ŅŃÖŖµćA£Ø2£¬1£©£¬OĪŖ×ų±źŌµć£®ĒėÄćŌŚ×ų±źÖįÉĻČ·¶ØµćP£¬Ź¹µĆ”÷AOP³ÉĪŖµČŃüČż½ĒŠĪ£®ŌŚøų³öµÄ×ų±źĻµÖŠ°ŃĖłÓŠÕāŃłµÄµćP¶¼ÕŅ³öĄ“£¬»ÉĻŹµŠÄµć£¬²¢ŌŚÅŌ±ß±źÉĻP1£¬P2£¬”£¬PKµÄ×ų±ź£ØÓŠkøö¾Ķ±źµ½PKĪŖÖ¹£¬²»±ŲŠ“³ö»·Ø£©£®
ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÄŚ£¬ŅŃÖŖµćA£Ø2£¬1£©£¬OĪŖ×ų±źŌµć£®ĒėÄćŌŚ×ų±źÖįÉĻČ·¶ØµćP£¬Ź¹µĆ”÷AOP³ÉĪŖµČŃüČż½ĒŠĪ£®ŌŚøų³öµÄ×ų±źĻµÖŠ°ŃĖłÓŠÕāŃłµÄµćP¶¼ÕŅ³öĄ“£¬»ÉĻŹµŠÄµć£¬²¢ŌŚÅŌ±ß±źÉĻP1£¬P2£¬”£¬PKµÄ×ų±ź£ØÓŠkøö¾Ķ±źµ½PKĪŖÖ¹£¬²»±ŲŠ“³ö»·Ø£©£®