题目内容
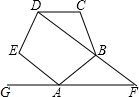如图，已知正五边形ABCDE，AF∥CD，交DB的延长线于点F，则∠DFA=考点：多边形内角与外角,平行线的性质
专题：
分析：首先求得正五边形内角∠C的度数，然后根据CD=CB求得∠CDB的度数，然后利用平行线的性质求得∠DFA的度数即可．
解答：解：∵正五边形的外角为360°÷5=72°，
∴∠C=180°-72°=108°，
∵CD=CB，
∴∠CDB=36°，
∵AF∥CD，
∴∠DFA=∠CDB=36°，
故答案为：36．
∴∠C=180°-72°=108°，
∵CD=CB，
∴∠CDB=36°，
∵AF∥CD，
∴∠DFA=∠CDB=36°，
故答案为：36．
点评：本题考查了多边形的内角和外角及平行线的性质，解题的关键是求得正五边形的内角．
练习册系列答案
金钥匙试卷系列答案
相关题目
