题目内容
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 ![]() (k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 ![]() (m为大于l的常数).记△CEF的面积为S1 , △OEF的面积为S2 , 则
(m为大于l的常数).记△CEF的面积为S1 , △OEF的面积为S2 , 则 ![]() = . (用含m的代数式表示)
= . (用含m的代数式表示)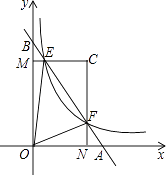
【答案】![]()
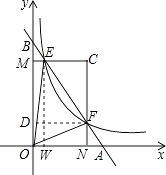
【解析】解:过点F作FD⊥BO于点D,EW⊥AO于点W,
∵ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵MEEW=FNDF,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
设E点坐标为:(x,my),则F点坐标为:(mx,y),
∴△CEF的面积为:S1= ![]() (mx﹣x)(my﹣y)=
(mx﹣x)(my﹣y)= ![]() (m﹣1)2xy,
(m﹣1)2xy,
∵△OEF的面积为:S2=S矩形CNOM﹣S1﹣S△MEO﹣S△FON ,
=MCCN﹣ ![]() (m﹣1)2xy﹣
(m﹣1)2xy﹣ ![]() MEMO﹣
MEMO﹣ ![]() FNNO,
FNNO,
=mxmy﹣ ![]() (m﹣1)2xy﹣
(m﹣1)2xy﹣ ![]() xmy﹣
xmy﹣ ![]() ymx,
ymx,
=m2xy﹣ ![]() (m﹣1)2xy﹣mxy,
(m﹣1)2xy﹣mxy,
= ![]() (m2﹣1)xy,
(m2﹣1)xy,
= ![]() (m+1)(m﹣1)xy,
(m+1)(m﹣1)xy,
∴ ![]() =
= 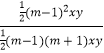 =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了反比例函数的图象和反比例函数的性质的相关知识点,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
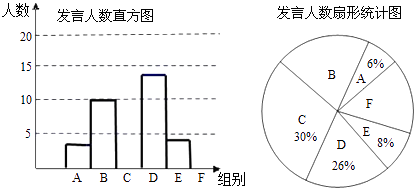
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
【题目】9岁的小芳身高1.36米,她的表姐明年想报考北京的大学.表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟,对北京有所了解.他们四人7月31日下午从苏州出发,1日到4日在北京旅游,8月5日上午返回苏州.
苏州与北京之间的火车票和飞机票价如下:火车 (高铁二等座) 全票524元,身高1.1~1.5米的儿童享受半价票;飞机 (普通舱) 全票1240元,已满2周岁未满12周岁的儿童享受半价票.他们往北京的开支预计如下:
住宿费 (2人一间的标准间) | 伙食费 | 市内交通费 | 旅游景点门票费 (身高超过1.2米全票) |
每间每天x元 | 每人每天100元 | 每人每天y元 | 每人每天120元 |
假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和,7月31日和8月5日合计按一天计算,不参观景点,但产生住宿、伙食、市内交通三项费用.
(1)他们往返都坐火车,结算下来本次旅游总共开支了13668元,求x,y的值;
(2)他们往返都坐飞机 (成人票五五折),其他开支不变,至少要准备多少元?
(3)他们去时坐火车,回来坐飞机 (成人票五五折),其他开支不变,准备了14000元,是否够用?如果不够,他们准备不再增加开支,而是压缩住宿的费用,请问他们预定的标准间房价每天不能超过多少元?