Question

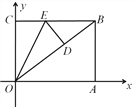
【题目】如图，将ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．

（1）求证：△ABF≌△ECF；

（2）若∠AFC=2∠D，连接AC、BE，求证：四边形ABEC是矩形．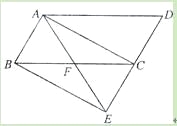

Answer 1

【答案】证明：（1）见解析

（2）见解析

【解析】

证明：(1)∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD．∴∠ABF＝∠ECF．

∵EC＝DC，∴AB＝EC．

在△ABF和△ECF中，∵∠ABF＝∠ECF，∠AFB＝∠EFC，AB＝EC，

∴△ABF≌△ECF．

(2)证法一：由(1)知AB＝EC，又AB∥EC，∴四边形ABEC是平行四边形．∴AF＝EF，BF＝CF．

∵四边形ABCD是平行四边形，∴∠ABC＝∠D，又∵∠AFC＝2∠D，∴∠AFC＝2∠ABC．

∵∠AFC＝∠ABF＋∠BAF，∴∠ABF＝∠BAF．∴FA＝FB．

∴FA＝FE＝FB＝FC，∴AE＝BC．∴□ABEC是矩形．

证法二：由(1)知AB＝EC，又AB∥EC，∴四边形ABEC是平行四边形．

∵四边形ABCD是平行四边形，∴AD∥BC，∴∠D＝∠BCE．

又∵∠AFC＝2∠D，∴∠AFC＝2∠BCE．

∵∠AFC＝∠FCE＋∠FEC，∴∠FCE＝∠FEC．∴∠D＝∠FEC．

∴AE＝AD．

又∵CE＝DC，∴AC⊥DE，即∠ACE＝90°．

∴□ABEC是矩形．