题目内容
已知等腰梯形的大底等于对角线的长,小底等于高,则该梯形的小底与大底的长度之比是
- A.3:5
- B.3:4
- C.2:3
- D.1:2
A
分析:先画出图形,设该梯形的小底与大底的长度分别为a,b,利用勾股定理求得a与b之间的关系,从而求出梯形的小底与大底的长度比.
解答:设该梯形的小底与大底的长度分别为a,b,过点D作DE∥AC,交BC的延长线于点E,

∴四边形ACED是平行四边形,
∴DE=b,DF=a,CF= (b-a),CE=a,
(b-a),CE=a,
由勾股定理得DF2+EF2=DE2,即a2+(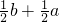 )2=b2,
)2=b2,
整理得5a2+2ab-3b2=0,利用十字相乘法分解因式得
(5a-3b)(a+b)=0
∴5a-3b=0
或a+b=0
即5a=3b
或a=-b
∵ab为线段的长,∴5a=3b,即a:b=3:5,
故选A.
点评:本题考查的知识点有:等腰梯形辅助线的作法,勾股定理.
分析:先画出图形,设该梯形的小底与大底的长度分别为a,b,利用勾股定理求得a与b之间的关系,从而求出梯形的小底与大底的长度比.
解答:设该梯形的小底与大底的长度分别为a,b,过点D作DE∥AC,交BC的延长线于点E,

∴四边形ACED是平行四边形,
∴DE=b,DF=a,CF=
 (b-a),CE=a,
(b-a),CE=a,由勾股定理得DF2+EF2=DE2,即a2+(
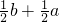 )2=b2,
)2=b2,整理得5a2+2ab-3b2=0,利用十字相乘法分解因式得
(5a-3b)(a+b)=0
∴5a-3b=0
或a+b=0
即5a=3b
或a=-b
∵ab为线段的长,∴5a=3b,即a:b=3:5,
故选A.
点评:本题考查的知识点有:等腰梯形辅助线的作法,勾股定理.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目



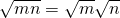 ;②
;②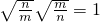 ;③
;③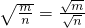 ;④
;④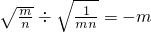 .
. 如图是一组数据的折线统计图,这组数据的方差是________.
如图是一组数据的折线统计图,这组数据的方差是________.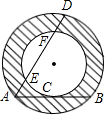 如图,一种圆管的横截面是同心圆的圆环面,大圆的弦AB切小圆于点C,大圆的弦AD交小圆于点E和F.为了计算截面的面积,甲、乙、丙三个同学分别用刻度尺测量出有关线段的长度:甲测得AB的长,乙测得AC的长,丙测得AD与EF的长.其中可以算出截面(图中阴影部分)面积的同学是
如图,一种圆管的横截面是同心圆的圆环面,大圆的弦AB切小圆于点C,大圆的弦AD交小圆于点E和F.为了计算截面的面积,甲、乙、丙三个同学分别用刻度尺测量出有关线段的长度:甲测得AB的长,乙测得AC的长,丙测得AD与EF的长.其中可以算出截面(图中阴影部分)面积的同学是 在图的几何体中,上下底面都是平行四边形,各个侧面都是梯形,那么图中和下底面平行的直线有
在图的几何体中,上下底面都是平行四边形,各个侧面都是梯形,那么图中和下底面平行的直线有