题目内容
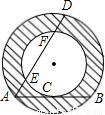
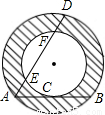
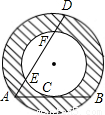
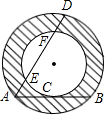如图，一种圆管的横截面是同心圆的圆环面，大圆的弦AB切小圆于点C，大圆的弦AD交小圆于点E和F．为了计算截面的面积，甲、乙、丙三个同学分别用刻度尺测量出有关线段的长度：甲测得AB的长，乙测得AC的长，丙测得AD与EF的长．其中可以算出截面（图中阴影部分）面积的同学是
- A.甲、乙
- B.乙、丙
- C.甲、丙
- D.甲、乙、丙
D
分析：根据勾股定理，将面积问题转化为线段长度平方的和差问题计算．
解答：
解：（1）连接OB、OC，
则πBO2-πOC2=π（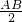
）2，
甲测得AB的长，可求出阴影面积；
（2）因为AC=CB=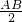，同（1）．
乙测得AC的长，可以算出截面面积；
（3）作OK⊥AD垂足为K，连接OD、OF，
因为πOD2-πOF2=π（OD2-OF2）=π（KD2+OK2-KF2-OK2）=π（KD2-KF2），
丙测得AD与EF的长，可以算出截面面积．
故选D．
点评：本题主要考查了将面积问题转化为线段长度平方的和差问题的能力．
分析：根据勾股定理，将面积问题转化为线段长度平方的和差问题计算．
解答：
解：（1）连接OB、OC，则πBO2-πOC2=π（
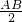）2，甲测得AB的长，可求出阴影面积；
（2）因为AC=CB=
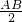，同（1）．乙测得AC的长，可以算出截面面积；
（3）作OK⊥AD垂足为K，连接OD、OF，
因为πOD2-πOF2=π（OD2-OF2）=π（KD2+OK2-KF2-OK2）=π（KD2-KF2），
丙测得AD与EF的长，可以算出截面面积．
故选D．
点评：本题主要考查了将面积问题转化为线段长度平方的和差问题的能力．
练习册系列答案
相关题目
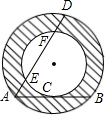如图，一种圆管的横截面是同心圆的圆环面，大圆的弦AB切小圆于点C，大圆的弦AD交小圆于点E和F．为了计算截面的面积，甲、乙、丙三个同学分别用刻度尺测量出有关线段的长度：甲测得AB的长，乙测得AC的长，丙测得AD与EF的长．其中可以算出截面（图中阴影部分）面积的同学是（ ）
