题目内容
(2008•房山区二模)已知:如图,AB是⊙O的直径,点C是⊙O上的一点,CD交AB的延长线于D,∠DCB=∠CAB.(1)求证:CD为⊙O的切线.
(2)若CD=4,BD=2,求⊙O的半径长.
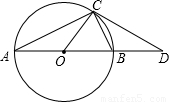
【答案】分析:(1)要证CD为⊙O的切线,只要证明OC⊥CD即可,由AB是⊙O的直径可得∠ACB=90°,只要∠DCB=∠ACO,由半径及已知∠DCB=∠CAB可得答案;
(2)可设出半径,用半径表示出OD,在直角三角形OCD中,利用勾股定理可求得半径的值.
解答:(1)证明:∵∠DCB=∠CAB,∠CAB=∠ACO,
∴∠DCB=∠ACO,
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠ACO+∠OCB=90°
∴∠DCB+∠OCB=90°,
∴∠OCD=90°
∴CD为⊙O的切线;
(2)解:设⊙O的半径为R,则OD=R+2,
∵CD=4,BD=2,∠OCD=90°,
由勾股定理得R2+42=(R+2)2,
解得:R=3,
∴⊙O的半径长为3.
点评:本题考查了切线的判断及性质及勾股定理的知识;证明过半径的外端点且垂直于这条半径的直线是圆的切线是常用的方法,求圆的半径常常用勾股定理,这些方法十分重要,要熟练掌握.
(2)可设出半径,用半径表示出OD,在直角三角形OCD中,利用勾股定理可求得半径的值.
解答:(1)证明:∵∠DCB=∠CAB,∠CAB=∠ACO,
∴∠DCB=∠ACO,
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠ACO+∠OCB=90°
∴∠DCB+∠OCB=90°,
∴∠OCD=90°
∴CD为⊙O的切线;
(2)解:设⊙O的半径为R,则OD=R+2,
∵CD=4,BD=2,∠OCD=90°,
由勾股定理得R2+42=(R+2)2,
解得:R=3,
∴⊙O的半径长为3.
点评:本题考查了切线的判断及性质及勾股定理的知识;证明过半径的外端点且垂直于这条半径的直线是圆的切线是常用的方法,求圆的半径常常用勾股定理,这些方法十分重要,要熟练掌握.

练习册系列答案
相关题目
 交于点A(1,m),求m及k的值.
交于点A(1,m),求m及k的值.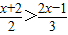 的正整数解.
的正整数解. +
+ .
.