��Ŀ����
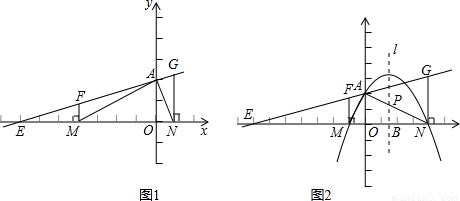
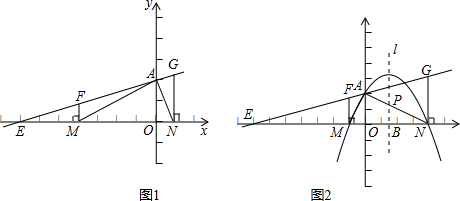
��ͼ1����ֱ֪��EA��x�ᡢy��ֱ��ڵ�E�͵�A��0��2������ֱ��EA�ϵ�����F��G�ֱ���x��Ĵ��߶Σ�����ֱ�ΪM��m��0����N��n��0��������m��0��n��0����1�����m=-4��n=1�����жϡ�AMN����״��
��2�����mn=-4����1�����йء�AMN����״�Ľ��ۻ������������������֤�����������������˵�����ɣ�
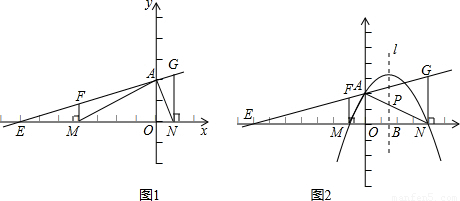
��3����ͼ2����Ŀ�е��������䣬���mn=-4������ON=4����M��A��N���������������Ӧ�ĺ�����ϵʽ��
��4���ڣ�3���������£���������ߵĶԳ���l���߶�AN���ڵ�P����Q�ǶԳ�����һ���㣬�Ե�P��Q��NΪ����������κ��Ե�M��A��NΪ��������������ƣ�����������ĵ�Q�����꣮
��������1�����ݹ��ɶ����������AM��AN��MN�ij��ȣ����ݹ��ɶ������涨���Ϳ��������������ֱ�������Σ�
��2��AM��AN��MN�ij��ȿ�����m��n��ʾ����������m��n�Ĺ�ϵ�Ϳ���֤����
��3��M��A��N��������֪�����ݴ���ϵ�����ֿ���������κ����Ľ���ʽ��
��4�������ߵĶԳ�����x��Ľ���Q1������������֤Rt��PNQ1��Rt��ANM��Rt��PQ2N��Rt��NQ2Q1��Rt��PNQ1��Rt��ANM�������ƣ��������������εĶ�Ӧ�ߵı���ȣ��õ�
=
�Ϳ������Q1Q2�õ����������ĵ�����꣮
��2��AM��AN��MN�ij��ȿ�����m��n��ʾ����������m��n�Ĺ�ϵ�Ϳ���֤����
��3��M��A��N��������֪�����ݴ���ϵ�����ֿ���������κ����Ľ���ʽ��
��4�������ߵĶԳ�����x��Ľ���Q1������������֤Rt��PNQ1��Rt��ANM��Rt��PQ2N��Rt��NQ2Q1��Rt��PNQ1��Rt��ANM�������ƣ��������������εĶ�Ӧ�ߵı���ȣ��õ�
| Q1Q2 |
| AN |
| Q1N |
| AM |
����⣺��1����AMN��ֱ�������Σ�
�������OA=2��OM=4��ON=1��
��MN=OM+ON=4+1=5
��Rt��AOM��AM=
=
=2
��Rt��AON��AN=
=
=
��MN2=AM2+AN2
���AMN��ֱ�������Σ��ⷨ��Ωһ������2�֣�
��2���𣺣�1���еĽ��ۻ�������
�������OA=2��OM=-m��ON=n
��MN=OM+ON=n-m
��MN2=��n-m��2=n2-2mn+m2
��mn=-4
��MN2=n2-2����-4��+m2=n2+m2+8
�֡���Rt��AOM�У�AM=
=
=
��Rt��AON��AN=
=
=
��AM2+AN2=4+m2+4+n2=n2+m2+8
��MN2=AM2+AN2
���AMN��ֱ�������Σ����ⷨ��Ωһ����2�֣�
��3����mn=-4��n=4��
��m=-1��
����һ���������ߵĺ�����ϵʽΪy=ax2+bx+c��
�������߾�����M��-1��0����N��4��0����A��0��2��
��
��
��
��
�����������ߵĺ�����ϵʽΪy=-
x2+
x+2��
���������������ߵĺ�����ϵʽΪy=a��x+1����x-4����
�������߾�����A��0��2��
��-4a=2���a=-
�����������ߵĺ�����ϵʽΪy=-
��x+1����x-4��
��y=-
x2+
x+2����2�֣�
��4�������ߵĶԳ�����x��Ľ���Q1����������
��l��MN����ANM=��PNQ1��
��Rt��PNQ1��Rt��ANM
�������ߵĶԳ���Ϊֱ��x=
��
��Q1��
��0����2�֣�
��NQ1=4-
=
��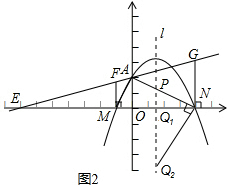
����N��NQ2��AN���������ߵĶԳ����ڵ�Q2��
��Rt��PQ2N��Rt��NQ2Q1��Rt��PNQ1��Rt��ANM��������
��
=
��Q1Q2=
•AN=
•
=5
�ߵ�Q2λ�ڵ������ޣ�
��Q2��
��-5����2�֣�
��ˣ����������ĵ���������
�ֱ���Q1��
��0����Q2��
��-5����
���ⷨ��Ωһ��
�������OA=2��OM=4��ON=1��
��MN=OM+ON=4+1=5
��Rt��AOM��AM=
| OA2+OM2 |
| 22+42 |
| 5 |
��Rt��AON��AN=
| OA2+ON2 |
| 22+12 |
| 5 |
��MN2=AM2+AN2
���AMN��ֱ�������Σ��ⷨ��Ωһ������2�֣�
��2���𣺣�1���еĽ��ۻ�������
�������OA=2��OM=-m��ON=n
��MN=OM+ON=n-m
��MN2=��n-m��2=n2-2mn+m2
��mn=-4
��MN2=n2-2����-4��+m2=n2+m2+8
�֡���Rt��AOM�У�AM=
| OA2+OM2 |
| 22+(-m)2 |
| 4+m2 |
��Rt��AON��AN=
| OA2+ON2 |
| 22+n2 |
| 4+n2 |
��AM2+AN2=4+m2+4+n2=n2+m2+8
��MN2=AM2+AN2
���AMN��ֱ�������Σ����ⷨ��Ωһ����2�֣�
��3����mn=-4��n=4��
��m=-1��
����һ���������ߵĺ�����ϵʽΪy=ax2+bx+c��
�������߾�����M��-1��0����N��4��0����A��0��2��
��
|
��
|
�����������ߵĺ�����ϵʽΪy=-
| 1 |
| 2 |
| 3 |
| 2 |
���������������ߵĺ�����ϵʽΪy=a��x+1����x-4����
�������߾�����A��0��2��
��-4a=2���a=-
| 1 |
| 2 |
�����������ߵĺ�����ϵʽΪy=-
| 1 |
| 2 |
��y=-
| 1 |
| 2 |
| 3 |
| 2 |
��4�������ߵĶԳ�����x��Ľ���Q1����������
��l��MN����ANM=��PNQ1��
��Rt��PNQ1��Rt��ANM
�������ߵĶԳ���Ϊֱ��x=
| 3 |
| 2 |
��Q1��
| 3 |
| 2 |
��NQ1=4-
| 3 |
| 2 |
| 5 |
| 2 |

����N��NQ2��AN���������ߵĶԳ����ڵ�Q2��
��Rt��PQ2N��Rt��NQ2Q1��Rt��PNQ1��Rt��ANM��������
��
| Q1Q2 |
| AN |
| Q1N |
| AM |
��Q1Q2=
| Q1N |
| AM |
| ||
|
| 22+42 |
�ߵ�Q2λ�ڵ������ޣ�
��Q2��
| 3 |
| 2 |
��ˣ����������ĵ���������
�ֱ���Q1��
| 3 |
| 2 |
| 3 |
| 2 |
���ⷨ��Ωһ��
������������Ҫ�����˹��ɶ������涨��������ϵ���������Ľ���ʽ���Լ����������ε����ʣ���Ӧ�ߵı���ȣ�

��ϰ��ϵ�д�
�����Ŀ