题目内容
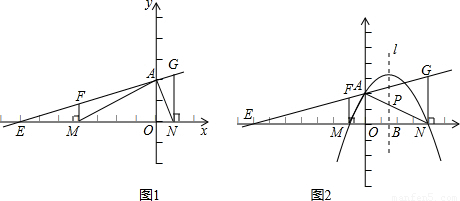
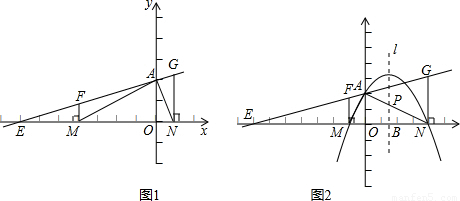
(2009•沧浪区一模)如图1,已知直线EA与x轴、y轴分别交于点E和点A(0,2),过直线EA上的两点F、G分别作x轴的垂线段,垂足分别为M(m,0)和N(n,0),其中m<0,n>0.(1)如果m=-4,n=1,试判断△AMN的形状;
(2)如果mn=-4,(1)中有关△AMN的形状的结论还成立吗?如果成立,请证明;如果不成立,请说明理由;
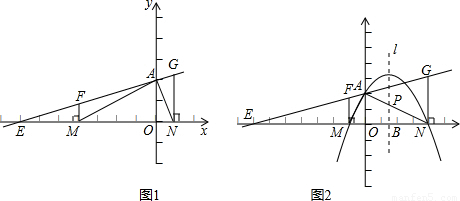
(3)如图2,题目中的条件不变,如果mn=-4,并且ON=4,求经过M、A、N三点的抛物线所对应的函数关系式;
(4)在(3)的条件下,如果抛物线的对称轴l与线段AN交于点P,点Q是对称轴上一动点,以点P、Q、N为顶点的三角形和以点M、A、N为顶点的三角形相似,求符合条件的点Q的坐标.
【答案】分析:(1)根据勾股定理可以求出AM.AN,MN的长度,根据勾股定理的逆定理就可以求出三角形是直角三角形.
(2)AM.AN,MN的长度可以用m,n表示出来,根据m,n的关系就可以证明.
(3)M、A、N的坐标已知,根据待定系数法局可以求出二次函数的解析式.
(4)抛物线的对称轴与x轴的交点Q1符合条件,易证Rt△PNQ1∽Rt△ANM且Rt△PQ2N、Rt△NQ2Q1、Rt△PNQ1和Rt△ANM两两相似,根据相似三角形的对应边的比相等,得到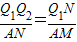 就可以求出Q1Q2得到符合条件的点的坐标.
就可以求出Q1Q2得到符合条件的点的坐标.
解答:解:(1)△AMN是直角三角形.
依题意得OA=2,OM=4,ON=1,
∴MN=OM+ON=4+1=5
在Rt△AOM中,AM=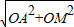 =
=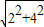 =
=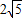
在Rt△AON中,AN=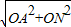 =
=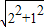 =
=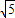
∴MN2=AM2+AN2
∴△AMN是直角三角形(解法不惟一).(2分)
(2)答:(1)中的结论还成立.
依题意得OA=2,OM=-m,ON=n
∴MN=OM+ON=n-m
∴MN2=(n-m)2=n2-2mn+m2
∵mn=-4
∴MN2=n2-2×(-4)+m2=n2+m2+8
又∵在Rt△AOM中,AM=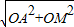 =
=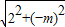 =
=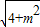
在Rt△AON中,AN=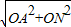 =
=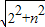 =
=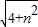
∴AM2+AN2=4+m2+4+n2=n2+m2+8
∴MN2=AM2+AN2
∴△AMN是直角三角形.(解法不惟一)(2分)
(3)∵mn=-4,n=4,
∴m=-1.
方法一:设抛物线的函数关系式为y=ax2+bx+c.
∵抛物线经过点M(-1,0)、N(4,0)和A(0,2)
∴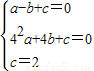 .
.
∴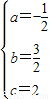 .
.
∴所求抛物线的函数关系式为y=- x2+
x2+ x+2.
x+2.
方法二:设抛物线的函数关系式为y=a(x+1)(x-4).
∵抛物线经过点A(0,2)
∴-4a=2解得a=-
∴所求抛物线的函数关系式为y=- (x+1)(x-4)
(x+1)(x-4)
即y=- x2+
x2+ x+2.(2分)
x+2.(2分)
(4)抛物线的对称轴与x轴的交点Q1符合条件,
∵l⊥MN,∠ANM=∠PNQ1,
∴Rt△PNQ1∽Rt△ANM
∵抛物线的对称轴为直线x= ,
,
∴Q1( ,0)(2分)
,0)(2分)
∴NQ1=4- =
= .
.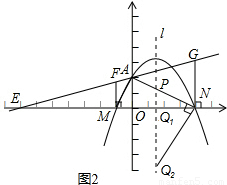
过点N作NQ2⊥AN,交抛物线的对称轴于点Q2.
∴Rt△PQ2N、Rt△NQ2Q1、Rt△PNQ1和Rt△ANM两两相似
∴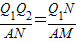
即Q1Q2=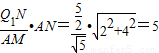
∵点Q2位于第四象限,
∴Q2( ,-5)(2分)
,-5)(2分)
因此,符合条件的点有两个,
分别是Q1( ,0),Q2(
,0),Q2( ,-5).
,-5).
(解法不惟一)
点评:本题主要考查了勾股定理的逆定理,待定系数法求函数的解析式.以及相似三角形的性质,对应边的比相等.
(2)AM.AN,MN的长度可以用m,n表示出来,根据m,n的关系就可以证明.
(3)M、A、N的坐标已知,根据待定系数法局可以求出二次函数的解析式.
(4)抛物线的对称轴与x轴的交点Q1符合条件,易证Rt△PNQ1∽Rt△ANM且Rt△PQ2N、Rt△NQ2Q1、Rt△PNQ1和Rt△ANM两两相似,根据相似三角形的对应边的比相等,得到
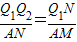 就可以求出Q1Q2得到符合条件的点的坐标.
就可以求出Q1Q2得到符合条件的点的坐标.解答:解:(1)△AMN是直角三角形.
依题意得OA=2,OM=4,ON=1,
∴MN=OM+ON=4+1=5
在Rt△AOM中,AM=
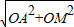 =
=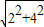 =
=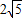
在Rt△AON中,AN=
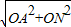 =
=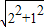 =
=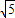
∴MN2=AM2+AN2
∴△AMN是直角三角形(解法不惟一).(2分)
(2)答:(1)中的结论还成立.
依题意得OA=2,OM=-m,ON=n
∴MN=OM+ON=n-m
∴MN2=(n-m)2=n2-2mn+m2
∵mn=-4
∴MN2=n2-2×(-4)+m2=n2+m2+8
又∵在Rt△AOM中,AM=
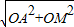 =
=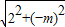 =
=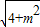
在Rt△AON中,AN=
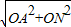 =
=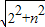 =
=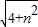
∴AM2+AN2=4+m2+4+n2=n2+m2+8
∴MN2=AM2+AN2
∴△AMN是直角三角形.(解法不惟一)(2分)
(3)∵mn=-4,n=4,
∴m=-1.
方法一:设抛物线的函数关系式为y=ax2+bx+c.
∵抛物线经过点M(-1,0)、N(4,0)和A(0,2)
∴
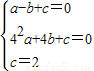 .
.∴
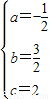 .
.∴所求抛物线的函数关系式为y=-
 x2+
x2+ x+2.
x+2.方法二:设抛物线的函数关系式为y=a(x+1)(x-4).
∵抛物线经过点A(0,2)
∴-4a=2解得a=-

∴所求抛物线的函数关系式为y=-
 (x+1)(x-4)
(x+1)(x-4)即y=-
 x2+
x2+ x+2.(2分)
x+2.(2分)(4)抛物线的对称轴与x轴的交点Q1符合条件,
∵l⊥MN,∠ANM=∠PNQ1,
∴Rt△PNQ1∽Rt△ANM
∵抛物线的对称轴为直线x=
 ,
,∴Q1(
 ,0)(2分)
,0)(2分)∴NQ1=4-
 =
= .
.
过点N作NQ2⊥AN,交抛物线的对称轴于点Q2.
∴Rt△PQ2N、Rt△NQ2Q1、Rt△PNQ1和Rt△ANM两两相似
∴
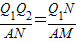
即Q1Q2=
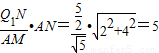
∵点Q2位于第四象限,
∴Q2(
 ,-5)(2分)
,-5)(2分)因此,符合条件的点有两个,
分别是Q1(
 ,0),Q2(
,0),Q2( ,-5).
,-5).(解法不惟一)
点评:本题主要考查了勾股定理的逆定理,待定系数法求函数的解析式.以及相似三角形的性质,对应边的比相等.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目