题目内容
抛物线y=x2+（2p+1）x+p2+p与x轴的交点情况是
- A.有两个不同的交点
- B.有一个交点
- C.无交点
- D.无法确定
A
分析：根据题意，令y=0，然后判断二次方程△的取值，即可确定交点情况．
解答：根据题意，令y=0，即x2+（2p+1）x+p2+p=0，
∴△=（2p+1）2-4（p2+p）
=4p2+4p+1-4p2-4p
=1＞0，
∴抛物线y=x2+（2p+1）x+p2+p与x轴有两个不同的交点，
故选A．
点评：本题考查了二次函数图象的特征以及二次函数与坐标轴交点情况的判断，需对二次函数图象的特征熟练理解应用．
分析：根据题意，令y=0，然后判断二次方程△的取值，即可确定交点情况．
解答：根据题意，令y=0，即x2+（2p+1）x+p2+p=0，
∴△=（2p+1）2-4（p2+p）
=4p2+4p+1-4p2-4p
=1＞0，
∴抛物线y=x2+（2p+1）x+p2+p与x轴有两个不同的交点，
故选A．
点评：本题考查了二次函数图象的特征以及二次函数与坐标轴交点情况的判断，需对二次函数图象的特征熟练理解应用．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
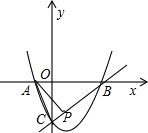A是抛物线与x轴的另一个交点．
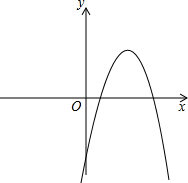已知一元二次方程-x2+bx+c=0的两个实数根是m，4，其中0＜m＜4．
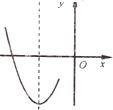16、已知抛物线y=x2+bx+c的部分图象如图所示，若方程x2+bx+c=0有两个同号的实数根，则c的值可以是