题目内容
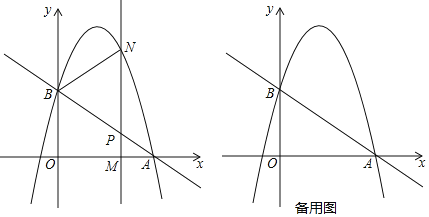
【题目】某游乐场每天的赢利额y(元)与售出的门票x(张)之间的函数关系如图所示.
(1)当0≤x≤200,且x为整数时,y关于x的函数解析式为【1】;当200≤x≤300,且x为整数时,y关于x的函数解析式为【2】;
(2)要使游乐场一天的赢利超过1000元,试问该天至少应售出多少张门票;
(3)请思考并解释图象与y轴交点(0,﹣1000)的实际意义;
(4)根据图象,请你再提供2条信息.

【答案】(1) y=10x﹣1000, y=15x﹣2500;(2)234;(3) 当每天不卖门票时,每天亏损1000元;(4)答案不唯一,合理即可,见解析.
【解析】分析:(1)根据图象可找到点,通过点的坐标可求出两段的解析式,都是一次函数.
(2)通过观察可知,应该是![]() ,应该用第二段.
,应该用第二段.
(3)如果有一天的门票为0的话,游乐园就会亏损1000元.如果一天卖出100张门票,则游乐场不盈利也不亏损;买200张门票时,还是采用0≤x≤200,游乐场会盈利1000元.
详解:(1)设![]() 时,y=kx1000,把(100,0)代入可得:0=100k1000,解得,k=10,那么可得函数式为:y=10x1000.
时,y=kx1000,把(100,0)代入可得:0=100k1000,解得,k=10,那么可得函数式为:y=10x1000.
设第二段范围的函数式为:y=kx+b,把(200,500)和(300,2000)代入可得:
![]() 解得
解得![]() ,即y=15x2500;
,即y=15x2500;
(2)∵y>1000,那么根据图象,则15x2500>1000,解得,![]() ,x取整则x=234(张).
,x取整则x=234(张).
(3)图象与y轴交点(0,1000)的实际意义为:当每天不卖门票时,每天亏损1000元.
(4)答案不唯一,合理即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如图,是一张平行四边形纸片ABCD,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
甲:连接AC,作AC的中垂线交AD、BC于E、F,则四边形AFCE是菱形. | 乙:分别作 |
对于甲、乙两人的作法,可判断( )

A.甲正确,乙错误B.甲错误,乙正确
C.甲、乙均正确D.甲、乙均错误