题目内容
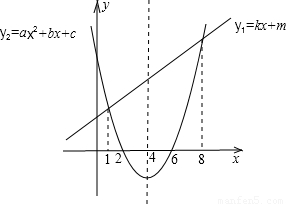
 20、有一次函数y1=kx+m和二次函数y2=ax2+bx+c的大致图象如图,请根据图中信息回答问题(在横线上直接写上答案)
20、有一次函数y1=kx+m和二次函数y2=ax2+bx+c的大致图象如图,请根据图中信息回答问题(在横线上直接写上答案)(1)不等式ax2+bx+c<0的解集是
2<x<6
;kx+m>ax2+bx+c的解集是1<x<8
.(2)当x=
1或8
时,y1=y2.(3)要使y2随x的增大而增大,x的取值范围应是
x>4
.分析:(1)由二次函数y2=ax2+bx+c与x轴的交点坐标为2、6;一次函数y1=kx+m和二次函数y2=ax2+bx+c交点的横坐标为1、8;即可得出;
(2)由一次函数y1=kx+m和二次函数y2=ax2+bx+c交点的横坐标为1、8,解答出即可;
(3)二次函数y2=ax2+bx+c的对称轴为x=4,结合图形,即可得出;
(2)由一次函数y1=kx+m和二次函数y2=ax2+bx+c交点的横坐标为1、8,解答出即可;
(3)二次函数y2=ax2+bx+c的对称轴为x=4,结合图形,即可得出;
解答:解:(1)如图,
∵二次函数y2=ax2+bx+c与x轴的交点坐标为2、6,
∴不等式ax2+bx+c<0的解集是:2<x<6;
∵一次函数y1=kx+m和二次函数y2=ax2+bx+c交点的横坐标为1、8,
∴kx+m>ax2+bx+c的解集是:1<x<8;
(2)∵一次函数y1=kx+m和二次函数y2=ax2+bx+c交点的横坐标为1、8,
∴当x=1或8时,y1=y2;
(3)∵二次函数y2=ax2+bx+c的对称轴为x=4,
∴当x>4时,y2随x的增大而增大.
故答案为:(1)2<x<6;1<x<8;(2)1或8;(3)x>4.
∵二次函数y2=ax2+bx+c与x轴的交点坐标为2、6,
∴不等式ax2+bx+c<0的解集是:2<x<6;
∵一次函数y1=kx+m和二次函数y2=ax2+bx+c交点的横坐标为1、8,
∴kx+m>ax2+bx+c的解集是:1<x<8;
(2)∵一次函数y1=kx+m和二次函数y2=ax2+bx+c交点的横坐标为1、8,
∴当x=1或8时,y1=y2;
(3)∵二次函数y2=ax2+bx+c的对称轴为x=4,
∴当x>4时,y2随x的增大而增大.
故答案为:(1)2<x<6;1<x<8;(2)1或8;(3)x>4.
点评:本题主要考查了一次函数和二次函数的图象与性质,体现了初中数学中的重要思想--数形结合思想.

练习册系列答案
相关题目
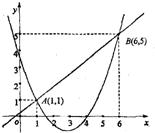 17、已知一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图所示,它们有两个交点A(1,1),B(6,5),那么能够使得y1>y2的自变量x的取值范围是
17、已知一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图所示,它们有两个交点A(1,1),B(6,5),那么能够使得y1>y2的自变量x的取值范围是 如图,一次函数y1=kx+1(k≠0)与反比例函数
如图,一次函数y1=kx+1(k≠0)与反比例函数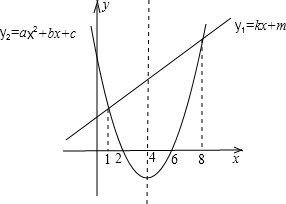 图中信息回答问题(在横线上直接写上答案)
图中信息回答问题(在横线上直接写上答案)