题目内容
如图，⊙O外接于△ABC，AD为⊙O的直径，∠ABC=20°，则∠CAD的度数为（ ）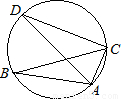
A．30°
B．40°
C．50°
D．70°
【答案】分析：根据圆周角定理，得∠ADC=20°，再根据AD是⊙O的直径，则∠ACD=90°，由三角形的内角和定理求得∠CAD的度数．
解答：解：∵∠ABC=20°，
∴∠ADC=20°，
∵AD是⊙O的直径，
∴∠ACD=90°，
∴∠CAD=90°-20°=70°．
故选D．
点评：本题考查了圆周角定理，直径所对的圆周角等于90°，以及三角形的内角和定理．
解答：解：∵∠ABC=20°，
∴∠ADC=20°，
∵AD是⊙O的直径，
∴∠ACD=90°，
∴∠CAD=90°-20°=70°．
故选D．
点评：本题考查了圆周角定理，直径所对的圆周角等于90°，以及三角形的内角和定理．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
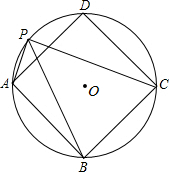如图，⊙O外接于边长为2的正方形ABCD，P为弧AD上一点，且AP=1，则
7、如图，⊙O外接于△ABC，AD为⊙O的直径，∠ABC=20°，则∠CAD的度数为（ ）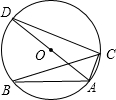
如图，⊙O外接于△ABC，AD为⊙O的直径，∠ABC=30°，则∠CAD的度数（ ）