题目内容
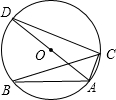如图，⊙O外接于△ABC，AD为⊙O的直径，∠ABC=30°，则∠CAD的度数（ ）分析：首先由∠ABC=30°，推出∠ADC=30°，然后根据AD为⊙O的直径，推出∠DCA=90°，最后根据直角三角形的性质即可推出∠CAD=90°-∠ADC，通过计算即可求出结果．
解答：解：∵∠ABC=30°，
∴∠ADC=30°，
∵AD为⊙O的直径，
∴∠DCA=90°，
∴∠CAD=90°-∠ADC=60°．
故选择D．
∴∠ADC=30°，
∵AD为⊙O的直径，
∴∠DCA=90°，
∴∠CAD=90°-∠ADC=60°．
故选择D．
点评：本题主要考查圆周角定理，直角三角形的性质，角的计算，关键在于通过相关的性质定理推出∠ADC和∠DCA的度数．
练习册系列答案
相关题目
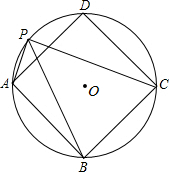如图，⊙O外接于边长为2的正方形ABCD，P为弧AD上一点，且AP=1，则
7、如图，⊙O外接于△ABC，AD为⊙O的直径，∠ABC=20°，则∠CAD的度数为（ ）
