题目内容
附加题:我们在前面学习过程中曾经接确过“弦图”,“弦图”是四个全等直角三角形与一个小正方形拼成的大正方形.你能用四个全等的直角三角形画出弦图吗?相信你肯定会了;那么请你根据你掌握的知识解决下面的问题,相信自己肯定能行!
(1)试用边长分别为1 cm和2 cm的2个正方形剪拼成一个大的正方形,并画出示意图.
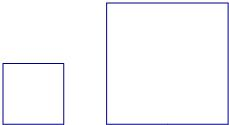
(2)下图是由5个相邻的正方形组成的一个长方形,试把它剪成一个正方形,画出示意图.

(3)请把一个宽为2,长为6.5的矩形纸片,剪拼成一个正方形,画出示意图.

分析:从题中把握信息并把得到的信息运用到题目中是关键,
(1)边长分别为1 cm和2 cm的2个正方形,则剪拼成一个大的正方形那么减拼后面积是不变的,则算出边长分别为1 cm和2 cm的2个正方形的面积之和为1×1+2×2=5,则可以减拼为边长为
cm的正方形;
(2)设小正方形的边长为x,则长方形的面积为5•x2,则大的正方形的面积为5•x2,边长为
•x
(3)可以求出矩形的面积为2×6.5=13,所以正方形的面积为13,边长为
.
(1)边长分别为1 cm和2 cm的2个正方形,则剪拼成一个大的正方形那么减拼后面积是不变的,则算出边长分别为1 cm和2 cm的2个正方形的面积之和为1×1+2×2=5,则可以减拼为边长为
| 5 |
(2)设小正方形的边长为x,则长方形的面积为5•x2,则大的正方形的面积为5•x2,边长为
| 5 |
(3)可以求出矩形的面积为2×6.5=13,所以正方形的面积为13,边长为
| 13 |
解答:解:(1)由题意可知S1=1cm2,S2=4cm2,则正方形的面积S=5cm2,边长为
cm,故它的图形如下:
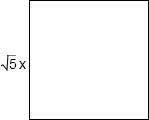
(2)从分析可知:5个相邻的正方形组成的一个长方形,试把它剪成一个正方形,正方形的面积为5•x2,边长为
•x,图形如下:
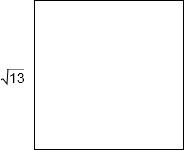
(3)由分析可知:正方形的面积为13,边长为
,故图形如下:
| 5 |

(2)从分析可知:5个相邻的正方形组成的一个长方形,试把它剪成一个正方形,正方形的面积为5•x2,边长为
| 5 |

(3)由分析可知:正方形的面积为13,边长为
| 13 |

点评:本题考查同学们对于正方形的性质的理解,即正方形的各边相等,面积为边长的平方.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
(本小题满分10分)
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
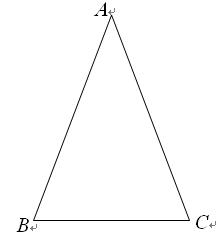
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=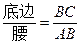 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad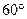 的值为( )
的值为( )
(2)对于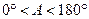 ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .
(3)已知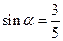 ,其中
,其中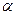 为锐角,试求sad
为锐角,试求sad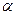 的值.
的值.
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
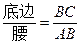 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:

(1)sad
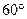 的值为( )
的值为( )A. | B.1 | C.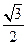 | D.2 |
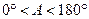 ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .(3)已知
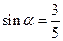 ,其中
,其中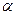 为锐角,试求sad
为锐角,试求sad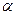 的值.
的值. 







