题目内容
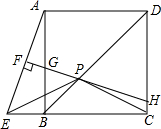 如图,正方形ABCD中,P在对角线BD上,E在CB的延长线上,且PE=PC,过点P作PF⊥AE于F,直线PF分别交AB、CD于G、H,
如图,正方形ABCD中,P在对角线BD上,E在CB的延长线上,且PE=PC,过点P作PF⊥AE于F,直线PF分别交AB、CD于G、H,(1)求证:DH=AG+BE;
(2)若BE=1,AB=3,求PE的长.
考点:正方形的性质,全等三角形的判定与性质,勾股定理
专题:压轴题
分析:(1)在DC上截取DM=BE,连接AM,证△ABE≌△ADM,推出∠1=∠2,推出AM⊥AE,推出AM∥FH,AB∥CD,得出四边形AGHM是平行四边形,推出AG=MH即可;
(2)连接AP.根据四边形ABCD是正方形的性质得出AB=BC,∠ABP=∠CBP=45°,证△ABP≌△CBP,推出PA=PC,∠3=∠4,求出∠3=∠5,得出△APE是等腰直角三角形,求出AE,即可求出PE.
(2)连接AP.根据四边形ABCD是正方形的性质得出AB=BC,∠ABP=∠CBP=45°,证△ABP≌△CBP,推出PA=PC,∠3=∠4,求出∠3=∠5,得出△APE是等腰直角三角形,求出AE,即可求出PE.
解答:(1)证明:在DC上截取DM=BE,连接AM,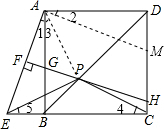
∵四边形ABCD是正方形,
∴∠ABE=∠ADM=90°,AB=AD,
∵在△ABE和△ADM中
,
∴△ABE≌ADM,
∴∠1=∠2,
∴∠1+∠BAM=∠2+∠BAM=90°,即AM⊥AE.
又∵PF⊥AE于F,
∴AM∥FH,
又∵AB∥CD,
∴四边形AGHM是平行四边形,
∴AG=MH,
∵DH=DM+MH,
∴DH=AG+BE.
(2)解:连接AP.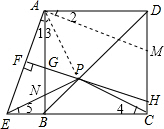
∵四边形ABCD是正方形,
∴AB=BC,∠ABP=∠CBP=45°,
∵在△ABP和△CBP中
∴△ABP≌△CBP,
∴PA=PC,∠3=∠4,
∵PE=PC,
∴PA=PE,
∵PE=PC,
∴∠4=∠5,
∴∠3=∠5,
又∵∠ANP=∠ENB,
∴∠3+∠ANP=∠5+∠ENB=90°,
∴AP⊥PE,即△APE是等腰直角三角形,
∵BE=1,AB=3,
∴AE=
=
,
∴PE=
=
=
.

∵四边形ABCD是正方形,
∴∠ABE=∠ADM=90°,AB=AD,
∵在△ABE和△ADM中
|
∴△ABE≌ADM,
∴∠1=∠2,
∴∠1+∠BAM=∠2+∠BAM=90°,即AM⊥AE.
又∵PF⊥AE于F,
∴AM∥FH,
又∵AB∥CD,
∴四边形AGHM是平行四边形,
∴AG=MH,
∵DH=DM+MH,
∴DH=AG+BE.
(2)解:连接AP.

∵四边形ABCD是正方形,
∴AB=BC,∠ABP=∠CBP=45°,
∵在△ABP和△CBP中
|
∴△ABP≌△CBP,
∴PA=PC,∠3=∠4,
∵PE=PC,
∴PA=PE,
∵PE=PC,
∴∠4=∠5,
∴∠3=∠5,
又∵∠ANP=∠ENB,
∴∠3+∠ANP=∠5+∠ENB=90°,
∴AP⊥PE,即△APE是等腰直角三角形,
∵BE=1,AB=3,
∴AE=
| 12+32 |
| 10 |
∴PE=
| AE | ||
|
| ||
|
| 5 |
点评:本题考查了正方形的性质和判定,勾股定理,等腰三角形性质,等腰直角三角形性质,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
小亮所在的九年级六班共有50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高是1.70米,而小亮的身高是1.75米,下列说法正确的是( )
| A、班上一定有25人身高低于1.70米 |
| B、这组身高数据的中位数一定是1.70米 |
| C、这组身高数据的众数一定不是1.75米 |
| D、1.70米是该班学生身高的平均水平 |
一个不透明的袋子里有4个颜色不同的球,其中2个红球,1个白球,1个黑球,搅匀后从袋里摸出两个球,摸到的两个球恰为一红一黑的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
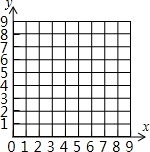 在平面直角坐标系xOy中,动点P从原点O出发,每次向上平移1个单位长度或向右平移2个单位长度,在上一次平移的基础上进行下一次平移.例如第1次平移后可能到达的点是(0,1)、(2,0),第2次平移后可能到达的点是(0,2)、(2,1)、(4,0),第3次平移后可能到达的点是(0,3)、(2,2)、(4,1)、(6,0),依此类推….我们记第1次平移后可能到达的所有点的横、纵坐标之和为l1,l1=3;第2次平移后可能到达的所有点的横、纵坐标之和为l2,l2=9;第3次平移后可能到达的所有点的横、纵坐标之和为l3,l3=18;按照这样的规律,
在平面直角坐标系xOy中,动点P从原点O出发,每次向上平移1个单位长度或向右平移2个单位长度,在上一次平移的基础上进行下一次平移.例如第1次平移后可能到达的点是(0,1)、(2,0),第2次平移后可能到达的点是(0,2)、(2,1)、(4,0),第3次平移后可能到达的点是(0,3)、(2,2)、(4,1)、(6,0),依此类推….我们记第1次平移后可能到达的所有点的横、纵坐标之和为l1,l1=3;第2次平移后可能到达的所有点的横、纵坐标之和为l2,l2=9;第3次平移后可能到达的所有点的横、纵坐标之和为l3,l3=18;按照这样的规律,