题目内容
11. 如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 根据等腰三角形两底角相等求出∠ABC的度数,再根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,根据等边对等角的性质可得∠ABD=∠A,然后求解即可.
解答 解:∵AB=AC,∠A=40°,
∴∠ABC=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-50°)=65°,
∵MN垂直平分线AB,
∴AD=BD,
∴∠ABD=∠A=50°,
∴∠DBC=∠ABC-∠ABD=65°-50°=15°.
故选A.
点评 本题主要考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形两底角相等的性质,等边对等角的性质,是基础题,熟记性质是解题的关键.

练习册系列答案
相关题目
3.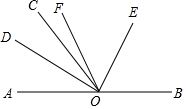 如图,O为直线AB上一点,过点O作直线OC,若∠AOC为锐角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE,则∠FOB+∠DOC的度数为( )
如图,O为直线AB上一点,过点O作直线OC,若∠AOC为锐角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE,则∠FOB+∠DOC的度数为( )
 如图,O为直线AB上一点,过点O作直线OC,若∠AOC为锐角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE,则∠FOB+∠DOC的度数为( )
如图,O为直线AB上一点,过点O作直线OC,若∠AOC为锐角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE,则∠FOB+∠DOC的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 135° |
20.现有四张分别标有数字1、2、2、3的卡片,他们除数字外完全相同.把卡片背面朝上洗匀,从中随机抽出一张后放回,再背朝上洗匀,从中随机抽出一张,则两次抽出的卡片所标数字不同的概率( )
| A. | $\frac{5}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{11}{16}$ | D. | $\frac{1}{2}$ |
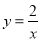 (x>0),
(x>0), (x>0)的图象上,且OA⊥OB,则
(x>0)的图象上,且OA⊥OB,则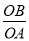 的值为( )
的值为( )
 B. 2 C.
B. 2 C.  D. 3
D. 3 如图,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=$\frac{25}{8}$π,S2=2π,则S3=$\frac{41}{8}π$.
如图,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=$\frac{25}{8}$π,S2=2π,则S3=$\frac{41}{8}π$.