题目内容
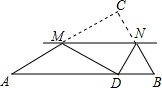（2012•资阳）如图，在△ABC中，∠C=90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC=6，NC=2| 3 |
分析：首先连接CD，交MN于E，由将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，即可得MN⊥CD，且CE=DE，又由MN∥AB，易得△CMN∽△CAB，根据相似三角形的面积比等于相似比的平方，相似三角形对应高的比等于相似比，即可得
=(
)2=
，又由MC=6，NC=2
，即可求得四边形MABN的面积．
| S△CMN |
| S△CAB |
| CE |
| CD |
| 1 |
| 4 |
| 3 |
解答：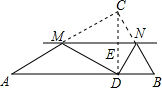
解：连接CD，交MN于E，
∵将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，
∴MN⊥CD，且CE=DE，
∴CD=2CE，
∵MN∥AB，
∴CD⊥AB，
∴△CMN∽△CAB，
∴
=(
)2=
，
∵在△CMN中，∠C=90°，MC=6，NC=2
，
∴S△CMN=
CM•CN=
×6×2
=6
，
∴S△CAB=4S△CMN=4×6
=24
，
∴S四边形MABN=S△CAB-S△CMN=24
-6
=18
．
故选C．
解：连接CD，交MN于E，∵将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，
∴MN⊥CD，且CE=DE，
∴CD=2CE，
∵MN∥AB，
∴CD⊥AB，
∴△CMN∽△CAB，
∴
| S△CMN |
| S△CAB |
| CE |
| CD |
| 1 |
| 4 |
∵在△CMN中，∠C=90°，MC=6，NC=2
| 3 |
∴S△CMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S△CAB=4S△CMN=4×6
| 3 |
| 3 |
∴S四边形MABN=S△CAB-S△CMN=24
| 3 |
| 3 |
| 3 |
故选C．
点评：此题考查了折叠的性质、相似三角形的判定与性质以及直角三角形的性质．此题难度适中，解此题的关键是注意折叠中的对应关系，注意数形结合思想的应用．
练习册系列答案
备战中考寒假系列答案
相关题目
（2012•资阳）如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（ ）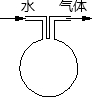
（2012•资阳）如图所示的球形容器上连接着两根导管，容器中盛满了不溶于水的比空气重的某种气体，现在要用向容器中注水的方法来排净里面的气体．水从左导管匀速地注入，气体从右导管排出，那么，容器内剩余气体的体积与注水时间的函数关系的大致图象是（ ）
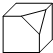（2012•资阳）如图是一个正方体被截去一角后得到的几何体，它的俯视图是（ ）
（2012•资阳）如图，在△ABC中，AB=AC，∠A=30°，以AB为直径的⊙O交BC于点D，交AC于点E，连接DE，过点B作BP平行于DE，交⊙O于点P，连接EP、CP、OP．