ЬтФПФкШн
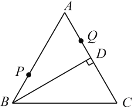
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() гы
гы![]() жсЃЌ
жсЃЌ![]() жсЗжБ№НЛгк
жсЗжБ№НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() Дг
Дг![]() ЕуГіЗЂЃЌбиЩфЯп
ЕуГіЗЂЃЌбиЩфЯп![]() ЕФЗНЯђдЫЖЏЃЌвбжЊ
ЕФЗНЯђдЫЖЏЃЌвбжЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌМЧ
ЃЌМЧ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНМА
ЕФКЏЪ§ЙиЯЕЪНМА![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉдкЭМ2ЫљЪОЕФЦНУцжБНЧзјБъЯЕжаЛГіЃЈ1ЃЉжаЫљЕУКЏЪ§ЕФЭМЯѓЃЌМЧЦфгы![]() жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ![]() ЃЌНЋИУЭМЯѓШЦЕу
ЃЌНЋИУЭМЯѓШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЃЌЛГіа§зЊКѓЕФЭМЯѓЃЛ
ЃЌЛГіа§зЊКѓЕФЭМЯѓЃЛ
ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯѓЃЌжБНгаДГіа§зЊЧАКѓЕФЭМЯѓгыжБЯп![]() ЕФНЛЕузјБъ.
ЕФНЛЕузјБъ.
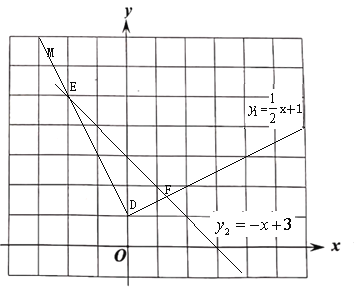
ЁОД№АИЁПЃЈ1ЃЉ![]() =
=![]() x+1(xЁн0)ЃЈ2ЃЉМћНтЮіЃЈ3ЃЉy2гыа§зЊЧАЕФЭМЯѓНЛгкЃЈ
x+1(xЁн0)ЃЈ2ЃЉМћНтЮіЃЈ3ЃЉy2гыа§зЊЧАЕФЭМЯѓНЛгкЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌy2гыа§зЊКѓЕФЭМЯѓНЛгкЃЈ-2,5ЃЉ.
ЃЉЃЌy2гыа§зЊКѓЕФЭМЯѓНЛгкЃЈ-2,5ЃЉ.
ЁОНтЮіЁП
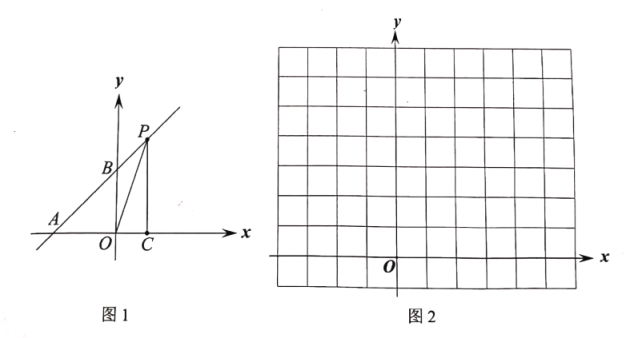
ЃЈ1ЃЉБэЪОГіPЕуЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЧѓНтЃЛ
ЃЈ2ЃЉИљОнжБНЧзјБъЯЕМДПЩзїЭМЃЛ
ЃЈ3ЃЉдкжБНЧзјБъЯЕжазїГіжБЯп![]() ЕФЭМЯёЃЌСЊСЂСНКЏЪ§МДПЩЧѓНт.
ЕФЭМЯёЃЌСЊСЂСНКЏЪ§МДПЩЧѓНт.
ЃЈ1ЃЉЁпЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌ
ЃЌ
ЁрPЃЈx,x+2ЃЉ(xЁн0)
Ёр![]() =SЁїCOP=
=SЁїCOP=![]() COЁСЃЈx+2ЃЉ=
COЁСЃЈx+2ЃЉ=![]() x+1(xЁн0)
x+1(xЁн0)
ЃЈ2ЃЉШчЭМЃЌзїГіКЏЪ§![]() =
=![]() x+1(xЁн0)ЕФЭМЯёШчЯТЃЌ
x+1(xЁн0)ЕФЭМЯёШчЯТЃЌ
ЩфЯпDMЮЊЫљЧѓЃЛ
ЃЈ3ЃЉзїжБЯп![]() ЕФЭМЯё
ЕФЭМЯё
СЊСЂ![]() =
=![]() x+1ЃЌ
x+1ЃЌ![]()
НтЕУx=![]() ,y=
,y=![]() МДFЃЈ
МДFЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
гЩЭМПЩжЊy2гыа§зЊКѓЕФЭМЯѓНЛЕуEЃЈ-2,5ЃЉ.
Ёрy2гыа§зЊЧАЕФЭМЯѓНЛгкЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌy2гыа§зЊКѓЕФЭМЯѓНЛгкЃЈ-2,5ЃЉ.
ЃЉЃЌy2гыа§зЊКѓЕФЭМЯѓНЛгкЃЈ-2,5ЃЉ.

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ