题目内容
已知函数y=| 2 | x |
(1)若这两个函数的图象都经过点(1,a),求a和k的值;
(2)当k取何值时,这两个函数的图象总有公共点.
分析:(1)因为这两个函数的图象都经过点(1,a),所以x=1,y=a是方程组
的解,代入可得a和k的值;
(2)要使这两个函数的图象总有公共点,须方程组
有解,即
=kx+1有解,根据判别式△即可求出K的取值范围.
|
(2)要使这两个函数的图象总有公共点,须方程组
|
| 2 |
| x |
解答:解:(1)∵两函数的图象都经过点(1,a),
∴
.
∴
.
(2)将y=
代入y=kx+1,消去y.得kx2+x-2=0.
∵k≠O,
∴要使得两函数的图象总有公共点,只要△≥0即可.
∴△=b2-4ac=1+8k≥0,
解得k≥-
;
∴k≥-
且k≠0.
∴
|
∴
|
(2)将y=
| 2 |
| x |
∵k≠O,
∴要使得两函数的图象总有公共点,只要△≥0即可.
∴△=b2-4ac=1+8k≥0,
解得k≥-
| 1 |
| 8 |
∴k≥-
| 1 |
| 8 |
点评:此题难度中等,考查了反比例函数、一次函数图象性质及一元二次方程判别式,综合性较强,同学们应熟练掌握.

练习册系列答案
相关题目
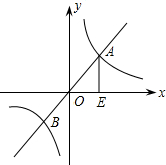 (2012•衢州)如图,已知函数y=2x和函数
(2012•衢州)如图,已知函数y=2x和函数