题目内容
如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连结BC,AF.
(1)求证:直线PA为⊙O的切线;
(2)若BC=6,![]() ∶
∶![]() =1∶2,求⊙O的半径的长.
=1∶2,求⊙O的半径的长.

解:(1)证明:如图,连接OB .
 ∵ PB是⊙O的切线,
∵ PB是⊙O的切线,
∴ ∠PBO=90°.
∵ OA=OB,BA⊥PO于D,
∴ AD=BD,∠POA=∠POB.
又∵ PO=PO,
∴ △PAO≌△PBO.
∴ ∠PAO=∠PBO=90°.
∴ 直线PA为⊙O的切线. ………………..2分
(2)∵ OA=OC,AD=BD,BC=6,
∴ OD=![]() BC=3.
BC=3.
设AD=x.
∵![]() ∶
∶![]() =1∶2,
=1∶2,
∴ FD=2x,OA=OF=2x-3.
在Rt△AOD中,由勾股定理 ,得(2x-3)2=x2+32.
解之得,x1=4,x2=0(不合题意,舍去).
∴ AD=4,OA=2x-3=5.
即⊙O的半径的长5. ………………..5分

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 (2013•孝感模拟)如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连接BC,AF.
(2013•孝感模拟)如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连接BC,AF.
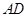 ∶
∶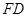 =1∶2,求⊙O的半径的长.
=1∶2,求⊙O的半径的长.
 ∶
∶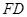 =1∶2,求⊙O的半径的长.
=1∶2,求⊙O的半径的长.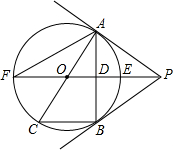 如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连接BC,AF.
如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连接BC,AF.