题目内容
如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连结BC,AF.
(1)求证:直线PA为⊙O的切线;
(2)若BC=6,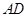 ∶
∶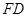 =1∶2,求⊙O的半径的长.
=1∶2,求⊙O的半径的长.
(1)连接OB,根据切线的性质可得∠PBO=90°,再有OA=OB,BA⊥PO于D,公共边PO可证得△PAO≌△PBO,即得∠PAO=∠PBO=90°,从而可以证得结论;(2)5
解析试题分析:(1)连接OB,根据切线的性质可得∠PBO=90°,再有OA=OB,BA⊥PO于D,公共边PO可证得△PAO≌△PBO,即得∠PAO=∠PBO=90°,从而可以证得结论;
(2)设AD=x,根据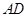 ∶
∶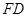 =1∶2,即可表示出FD=2x,OA=OF=2x-3,在Rt△AOD中,根据勾股定理即可列方程求解.
=1∶2,即可表示出FD=2x,OA=OF=2x-3,在Rt△AOD中,根据勾股定理即可列方程求解.
(1)如图,连接OB 
∵PB是⊙O的切线
∴∠PBO=90°
∵OA=OB,BA⊥PO于D
∴AD=BD,∠POA=∠POB
又∵PO=PO
∴△PAO≌△PBO
∴∠PAO=∠PBO=90°
∴直线PA为⊙O的切线;
(2)∵OA=OC,AD=BD,BC=6
∴OD= BC=3
BC=3
设AD=x
∵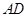 ∶
∶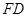 =1∶2
=1∶2
∴FD=2x,OA=OF=2x-3
在Rt△AOD中,由勾股定理得(2x-3)2=x2+32
解得x1=4,x2=0(不合题意,舍去)
∴AD=4,OA=2x-3=5
即⊙O的半径的长5.
考点:切线的性质,全等三角形的判定和性质,勾股定理
点评:解答本题的关键是熟练掌握切线垂直于经过切点的半径,注意勾股定理在圆中的灵活应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•孝感模拟)如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连接BC,AF.
(2013•孝感模拟)如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连接BC,AF.
 ∶
∶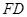 =1∶2,求⊙O的半径的长.
=1∶2,求⊙O的半径的长.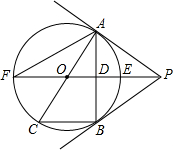 如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连接BC,AF.
如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连接BC,AF.