题目内容
在平面直角坐标系内，直线y=
x+3与两坐标轴交于A、B两点，点O为坐标原点，若在该坐标平面内有以点P（不与点A、B、O重合）为顶点的直角三角形与Rt△ABO全等，且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边，则所有符合条件的P点个数为（ ）
| 3 |
| 4 |
| A、9个 | B、7个 | C、5个 | D、3个 |
分析：分别以直角三角形的一直角边为公共边，过直角边的两顶点作垂线，在此垂线上截取线段使线段的长等于另一直角边，连接此点与另一端点的连线即可；在以公共斜边作直角三角形时要以AB为直径作圆，再在圆上找出与A、B两点的连线等于两直角边的点即可．
解答：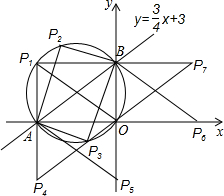
解：如图，图中的P1、P2、P3、P4、P5、P6、P7，就是符合要求的点P，
注意以P1为公共点的直角三角形有3个．?
故选B．
解：如图，图中的P1、P2、P3、P4、P5、P6、P7，就是符合要求的点P，注意以P1为公共点的直角三角形有3个．?
故选B．
点评：此题综合考查一次函数的图象与两坐标轴的交点的求法，直角三角形全等的判定．
练习册系列答案
名校课堂系列答案
相关题目
在平面直角坐标系内，已知点A（2，1），O为坐标原点．请你在坐标轴上确定点P，使得△AOP成为等腰三角形．在给出的坐标系中把所有这样的点P都找出来，画上实心点，并在旁边标上P1，P2，…，PK的坐标（有k个就标到PK为止，不必写出画法）．