题目内容
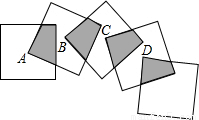
将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,(以下有(1)、(2)两问,每个考生只须选答一问,若两问都答,则只以第(2)问 计分)
计分)
(1)第一问:图中△AMN的面积是________;
(2)第二问:图中四块阴影面积的和为________.
解:(1)∵点A是正方形的中心,
∴点A到MN的距离等于边长的 ,即1cm,
,即1cm,
∴△AMN的面积= ×2×1=1cm2;
×2×1=1cm2;
(2)如图,过B作分别作正方形两边的垂线,垂足分别为E、G,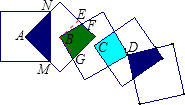
∴∠BEF=∠BGH=90°,BE=BG=1cm,∠FBG=90°,
∵∠EBF+∠FBG=90°,∠FBG+∠GBH=90°,
∴∠EBF=∠GBH,
在△BEF与△BGH中, ,
,
∴△BEF≌△BGH(AAS),
∴S△BEF=S△BGH,
∴阴影部分的面积=1×1=1cm2,
同理可证,其它阴影部分的面积都是1cm2,
∴四块阴影面积的和为:1×4=4cm2.
故答案为:(1)1cm2,4cm2.
分析:(1)根据正方形中心到边长的距离等于边长的一半,利用三角形的面积公式求解即可;
(2)如图,过B作分别作正方形两边的垂线,垂足分别为E、G,然后证明△BEF与△BGH全等,从而得出阴影部分的面积等于正方形面积的 ,同理可证其它阴影部分面积都是正方形面积的
,同理可证其它阴影部分面积都是正方形面积的 ,据此得解.
,据此得解.
点评:本题主要考查了正方形的性质及面积公式,解答本题的关键是作出辅助线利用三角形全等把不规则的阴影部分的面积转化为规则的四边形的面积,即以正方形的中心与一个顶点为两顶点的正方形的面积,实际上也就是每个阴影部分的面积都等于正方形面积的 .
.
∴点A到MN的距离等于边长的
 ,即1cm,
,即1cm,∴△AMN的面积=
 ×2×1=1cm2;
×2×1=1cm2;(2)如图,过B作分别作正方形两边的垂线,垂足分别为E、G,

∴∠BEF=∠BGH=90°,BE=BG=1cm,∠FBG=90°,
∵∠EBF+∠FBG=90°,∠FBG+∠GBH=90°,
∴∠EBF=∠GBH,
在△BEF与△BGH中,
 ,
,∴△BEF≌△BGH(AAS),
∴S△BEF=S△BGH,
∴阴影部分的面积=1×1=1cm2,
同理可证,其它阴影部分的面积都是1cm2,
∴四块阴影面积的和为:1×4=4cm2.
故答案为:(1)1cm2,4cm2.
分析:(1)根据正方形中心到边长的距离等于边长的一半,利用三角形的面积公式求解即可;
(2)如图,过B作分别作正方形两边的垂线,垂足分别为E、G,然后证明△BEF与△BGH全等,从而得出阴影部分的面积等于正方形面积的
 ,同理可证其它阴影部分面积都是正方形面积的
,同理可证其它阴影部分面积都是正方形面积的 ,据此得解.
,据此得解.点评:本题主要考查了正方形的性质及面积公式,解答本题的关键是作出辅助线利用三角形全等把不规则的阴影部分的面积转化为规则的四边形的面积,即以正方形的中心与一个顶点为两顶点的正方形的面积,实际上也就是每个阴影部分的面积都等于正方形面积的
 .
. 
练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
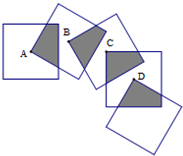 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )| A、2cm2 | B、4cm2 | C、6cm2 | D、8cm2 |
 计分)
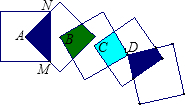
计分)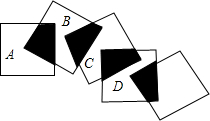 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是正方形的中心,则图中四块阴影部分的面积和为
将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是正方形的中心,则图中四块阴影部分的面积和为