题目内容
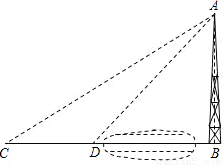
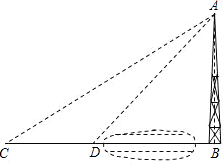
如图，河对岸有水塔AB．在河边D处测得塔顶A的仰角为60°，然后沿直线BD后退18米到点C，在C处测得塔顶A的仰角为45°，求水塔高．
【答案】分析：设AB=x，然后用x通过三角函数关系表示出BD和CB，BC-BD=CD=18可得出x的值．
解答：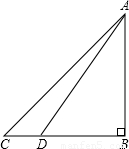
解：依题意，可得如图所示的△ABC中，∠B=90°，∠ADB=60°，∠C=45°，DC=18．
设AB=x，
∵∠C=45°，
∴AB=CB=x，
∴DB=x-18．
在Rt△ABD中，∠ADB=60°，
∵tan60°=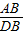
，
∴
．
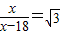∴x=27+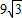
．所以水塔高为（27+
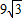）米．
点评：本题考查解直角三角形的应用，要注意仔细计算．
解答：
解：依题意，可得如图所示的△ABC中，∠B=90°，∠ADB=60°，∠C=45°，DC=18．设AB=x，
∵∠C=45°，
∴AB=CB=x，
∴DB=x-18．
在Rt△ABD中，∠ADB=60°，
∵tan60°=
，∴
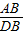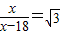．∴x=27+
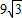．所以水塔高为（27+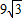）米．点评：本题考查解直角三角形的应用，要注意仔细计算．
练习册系列答案
相关题目
引进一个或两个中间量．以此作为媒介，再寻找这些量之间的关系，得到．于是，就可求得水塔的高，问题就解决了．
如图，河对岸有水塔AB．在河边D处测得塔顶A的仰角为60°，然后沿直线BD后退18米到点C，在C处测得塔顶A的仰角为45°，求水塔高．
如图，河对岸有水塔AB．在河边D处测得塔顶A的仰角为60°，然后沿直线BD后退18米到点C，在C处测得塔顶A的仰角为45°，求水塔高．