Question

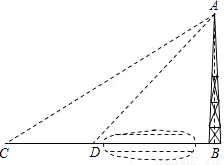
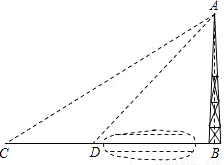
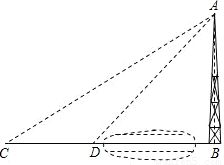
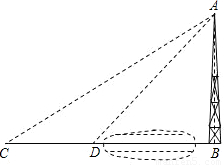
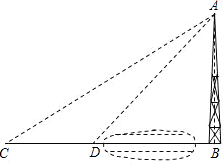
课本中有这么一个例题：“如图，河对岸有一水塔AB．在C处测得塔顶A的仰角为30°，向塔前进12米到达D，在D处测得A的仰角为45°，求水塔AB的高”．
解这个题时，我们通常时这样去想的（分析）：要求水塔AB的高，只要去寻找AB于已知量之间的关系．在这里，由于难以找到四个量之间的直接关系，我们可引进一个或两个中间量．以此作为媒介，再寻找这些量之间的关系，得到．于是，就可求得水塔的高，问题就解决了．

Answer 1

分析：图中有两个直角三角形，利用公共边AB表示出BC，BD，再根据CD=BC-BD，即可求得AB的长．

解答：解：根据题意，
在直角△ABC中，BC=

AB

tan30°

=

3

AB，
在直角△ABD中，BD=

AB

tan45°

=AB，
∵CD=BC-BD=12，
∴（

3

-1）AB=12；
解之得AB=6（

3

+1）米．

点评：通过公共边建立相关线段的联系是解决综合题的常规思路．