题目内容
观察下列方程和等式,寻找规律,完成问题:①方程x2-7x+6=0,x1=1,x2=6,而x2-7x+6=(x-1)(x-6);
②方程x2-4x-5=0,x1=5,x2=-1,而x2-4x-5=(x-5)(x+1);
③方程4x2-12x+9=0,
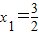 ,
,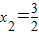 ,而
,而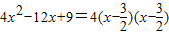 ;
;④方程3x2+7x+4=0,
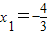 ,x2=-1,而
,x2=-1,而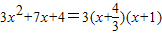 ;…
;…(1)探究规律:当方程ax2+bx+c=0(a≠0)时,______
【答案】分析:(1)求出一元二次方程的根即可进行因式分解;
(2)利用x2-x-2=0,根为x1=2,x2=-1,以及2x2+3x-2=0,得出x1=-2,x2= ,进而因式分解即可;
,进而因式分解即可;
(3)根据2a2+5a+2=0,得出x1=- ,x2=-2,即可得出此矩形的长和宽.
,x2=-2,即可得出此矩形的长和宽.
解答:解:(1)∵方程ax2+bx+c=0,
方程的根为:x=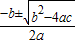 ,
,
∴ax2+bx+c=(x-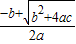 )(x-
)(x-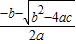 );
);
(2)∵x2-x-2=0,
x1=2,x2=-1,
∴x2-x-2;
=(x-2)(x+1);
∵2x2+3x-2=0,
x1=-2,x2= ,
,
∴2x2+3x-2,
=(x+2)(2x-1);
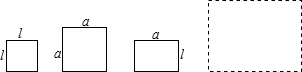
(3)2a2+5a+2=0,
x1=- ,x2=-2,
,x2=-2,
∴2a2+5a+2,
=(2a+1)(a+2),
∴此矩形的长和宽分别为:2a+1,a+2.
点评:此题主要考查了因式分解的应用,根据已知得出求出方程的根是解题关键.
(2)利用x2-x-2=0,根为x1=2,x2=-1,以及2x2+3x-2=0,得出x1=-2,x2=
 ,进而因式分解即可;
,进而因式分解即可;(3)根据2a2+5a+2=0,得出x1=-
 ,x2=-2,即可得出此矩形的长和宽.
,x2=-2,即可得出此矩形的长和宽.解答:解:(1)∵方程ax2+bx+c=0,
方程的根为:x=
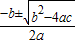 ,
,∴ax2+bx+c=(x-
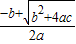 )(x-
)(x-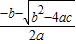 );
);(2)∵x2-x-2=0,
x1=2,x2=-1,
∴x2-x-2;
=(x-2)(x+1);
∵2x2+3x-2=0,
x1=-2,x2=
 ,
,∴2x2+3x-2,
=(x+2)(2x-1);
(3)2a2+5a+2=0,
x1=-
 ,x2=-2,
,x2=-2,∴2a2+5a+2,
=(2a+1)(a+2),
∴此矩形的长和宽分别为:2a+1,a+2.
点评:此题主要考查了因式分解的应用,根据已知得出求出方程的根是解题关键.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 ,
,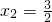 ,而
,而 ;
; ,x2=-1,而
,x2=-1,而 ;…
;…