题目内容
下列结论正确的个数是（ ）
①两条直角边对应相等的两个直角三角形全等
②底边相等，且周长相等的两个等腰三角形全等；
③腰长相等，且有一角是50°的两个等腰三角形全等；
④有两边及其中一边上的高对应相等的两个三角形全等．
①两条直角边对应相等的两个直角三角形全等
②底边相等，且周长相等的两个等腰三角形全等；
③腰长相等，且有一角是50°的两个等腰三角形全等；
④有两边及其中一边上的高对应相等的两个三角形全等．
分析：根据全等三角形的判定定理，结合各项进行判断即可．
解答：解：①两条直角边对应相等的两个直角三角形全等，说法正确；可用SAS判定全等；
②底边相等，且周长相等的两个等腰三角形全等，说法正确；可用SSS判定全等；
③腰长相等，且有一角是50°的两个等腰三角形全等，说法错误；
④有两边及其中一边上的高对应相等的两个三角形不一定全等，
如图：△ABC和△ACD，的边CB=CA，CA=CD，高AE=AE，
但△ABC和△ACD不全等，故说法错误；
综上可得①②正确，共2个．
故选B．
②底边相等，且周长相等的两个等腰三角形全等，说法正确；可用SSS判定全等；
③腰长相等，且有一角是50°的两个等腰三角形全等，说法错误；
④有两边及其中一边上的高对应相等的两个三角形不一定全等，
如图：△ABC和△ACD，的边CB=CA，CA=CD，高AE=AE，
但△ABC和△ACD不全等，故说法错误；
综上可得①②正确，共2个．
故选B．
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
练习册系列答案
相关题目
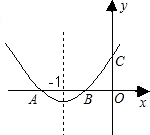已知：如图所示，抛物线y=ax2+bx+c的对称轴为x=-1，与x轴交于A、B两点，交y轴于点C，且OB=OC，则下列结论正确的个数是（ ）
9、如图，AB⊥BD，EB⊥BC，∠5=∠6，则下列结论正确的个数是（ ）