Question

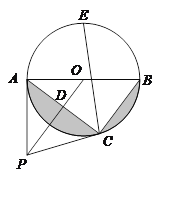
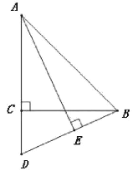
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D为AC延长线上一点,连接BD,AE⊥BD于点E.

(1)记△ABC得外接圆为⊙0,

①请用文字描述圆心0的位置;

②求证:点E一定在⊙0上.

(2)将射线AE绕点A顺时针旋转45°后,所得到的射线与BD延长线交于点F,连接CF,CE.

①依题意补全图形;

②用等式表示线段AF,CE,BE的数量关系,并证明.

Answer 1

【答案】（1）证明见解析（2）AF=2CE+BE

【解析】

(1)连接OC,OE, 可得OC=OE=OA=OB=AB,即点E在以O为圆心,OA为半径的圆上,

即点E在△ABC的外接圆⊙O上.

(2) 过点C作CG⊥CE,与BF交于点G,可证的∠BCG=∠ECA及△ACE≌△BCG(ASA)，可得BG=AE,EC=GC，由旋转的性质可得∠EFA=90°-∠EAF=45°=∠EAF,AE=EF，可得AF=2CE+BE.

(1)①线段AB的中点;

②证明:如图,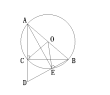

连接OC,OE,

∵AE⊥BD,

∴∠AEB=90°,

∵∠ACB=90°,O为AB中点,

∴OC=OE=OA=OB=AB,

∴点E在以O为圆心,OA为半径的圆上,

即点E在△ABC的外接圆⊙O上.

(2)①如上图中所示,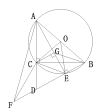

②AF=2CE+BE;

证明如下:

过点C作CG⊥CE,与BF交于点G.

∴∠ECG=∠BCA=90°,

∴∠ECG+∠BCE=∠BCA+∠BCE,

即∠BCG=∠ECA.

∵E,A,B,C在以O为圆心,OA为半径的圆上,

∴∠EAC=∠EBC.

∵BC=AC,

∴△ACE≌△BCG(ASA)

∴BG=AE,EC=GC.

∴在Rt△CEG中,EG=.

∵由旋转,∠EAF=45°,而∠AEF=90°,

∴∠EFA=90°-∠EAF=45°=∠EAF,

∴AE=EF，

∴在Rt△AEF中,AF=.

∵BG=BE+EG=BE+CE,

∴AF=2CE+BE.