题目内容
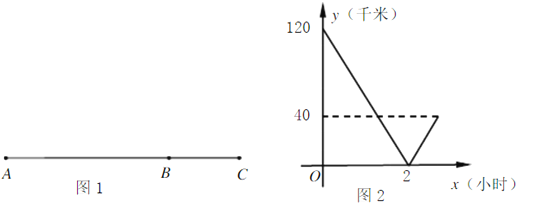
【题目】如图1,元旦期间,小明乘汽车从![]() 地出发,经过
地出发,经过![]() 地到目的地
地到目的地![]() 地(三地在同一条直线上),假设汽车从
地(三地在同一条直线上),假设汽车从![]() 到
到![]() 的过程都是匀速直线行驶.图2表示小明离
的过程都是匀速直线行驶.图2表示小明离![]() 地的路程
地的路程![]() (km)与汽车从
(km)与汽车从![]() 出发后行驶时间
出发后行驶时间![]() (h)之何的函数关系图象.
(h)之何的函数关系图象.
(1) ![]() 两地间的路程为 km;
两地间的路程为 km;
(2)求小明离![]() 地的路程
地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(3)当行驶时间![]() 在什么范围时,汽车离
在什么范围时,汽车离![]() 地的路程不超过40 km?
地的路程不超过40 km?
【答案】(1) 160;(2)当![]() 时,表达式为:
时,表达式为:![]() ; 当
; 当![]() 时,表达式为:
时,表达式为:![]() ;(3)
;(3) ![]() .
.
【解析】
(1)观察图象可知A地到B地的距离为120km,B地到C地的距离是40km,由此即可得答案;
(2)先求出汽车的速度,然后求出到C地所用的时间,然后分0≤x≤2和2<x≤![]() 两种情况进行求解即可;
两种情况进行求解即可;
(3)将y=40代入(2)中的解析式进行求解即可得.
(1)观察图象可知A地到B地的距离是120km,B地到C地的距离是40km,
所以A、C两地间的距离是120+40=160km,
故答案为:160;
(2)汽车的速度为:120÷2=60km/h,
汽车从A地到C地所用时间为:160÷60=![]() h,
h,
当0≤x≤2时,设解析式为y=k1x+b1,
将(0,120)、(2,0)分别代入得![]() ,
,
解得:![]() ,
,
所以当0≤x≤2时,解析式为y=-60x+120,
当2<x≤![]() 时,设解析式为y=k2x+b2,
时,设解析式为y=k2x+b2,
将(2,0)、(![]() ,40)分别代入得
,40)分别代入得 ,
,
解得:![]() ,
,
所以当2<x≤![]() 时,解析式为y=60x-120;
时,解析式为y=60x-120;
(3)把y=40代入y=-60x+120,得40=-60x+120,
解得:x=![]() ,
,
把y=40代入y=60x-120,得40=60x-120,
解得:x=![]() ,
,
所以当行驶时间![]() 在
在![]() 范围时,汽车离
范围时,汽车离![]() 地的路程不超过40 km.
地的路程不超过40 km.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】实验中学学生会倡议同学们将用不着的课外书籍捐赠给希望小学.学生会对全校的捐赠情况进行调查和分组统计后,将数据整理成如图所示统计图(图中信息不完整).已知A组和B组的人数比为1:5.
捐书人数分组统计表
组别 | 捐书数量x/本 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | x≥40 |
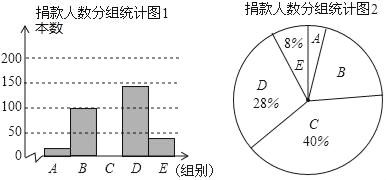
请结合以上信息解答下列问题:
(1)a= ,本次参加捐书的总人数是 ;
(2)先求出C组的人数,再补全“捐书人数分组统计图1”;
(3)扇形统计图中,B组所对应的圆心角的度数是 .