Question

【题目】如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足CF∶DF=1∶3，连接AF并延长交⊙O于点E，连接AD、DE，若CF=3，AF=4.

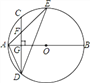
（1）求证：△ADF∽△AED；

（2）求FG的长；

（3）求tan∠E的值．

Answer 1

【答案】(1)见解析;(2)3;(3) .

【解析】分析：（1）由AB是⊙O的直径，弦CD⊥AB，根据垂径定理可得弧AD=弧AC，所以∠ADC=∠E，又因∠FAD=∠DAE，继而证得△ADF∽△AED；（2）因CD⊥AB，根据垂径定理可得CG=DG，再由GF∶DF=1∶3，CF=3，可得FD=9，从而求得CD= 12，所以CG=DG=6，继而得FG=3；（3）在Rt△AFG中，AF=4，FG=3，根据勾股定理可得，由（1）知∠ADC=∠E，所以.

详解：

（1）证明：∵AB是⊙O的直径，CD⊥AB，
∴ ，∴∠ADC=∠E，

而∠FAD=∠DAE，∴△ADF∽△AED，

（2）∵CD⊥AB，∴CG=DG，
∵GF∶DF=1∶3，CF=3，∴FD=3CF=9，

∴CD=CF+FD=12， ∴CG=DG=6，

∴FG=CG-CF=3，

（3）在Rt△AFG中，AF=4，FG=3，
∴，

由（1）知∠ADC=∠E，∴.