题目内容
已知关于x的方程kx2+(k+2)x+| k |
| 4 |
(1)求实数k的取值范围;
(2)设方程的两实根为x1和x2(x1≠x2),那么是否存在实数k,使
| 1 |
| x1 |
| 1 |
| x2 |
分析:(1)由于x的方程kx2+(k+2)x+
=0有两个不相等的实数根,那么方程的判别式大于0,且k≠0,由此可求出实数k的取值范围;
(2)根据根与系数的关系可以得到两根之和与两根之积,然后把已知等式变形为和两根之和与两根之积相关的形式,再代入即可得到关于k的方程,也可以判断是否存在实数k,使
+
=2成立.
| k |
| 4 |
(2)根据根与系数的关系可以得到两根之和与两根之积,然后把已知等式变形为和两根之和与两根之积相关的形式,再代入即可得到关于k的方程,也可以判断是否存在实数k,使
| 1 |
| x1 |
| 1 |
| x2 |
解答:解:(1)由△=(k+2)2-4k×
>0,
解得k>-1,
又∵k≠0,
∴k的取值范围是k>-1且k≠0;
(2)不存在符合条件的实数k,
理由如下:
∵x1+x2=-
,x1x2=
,
又
+
=
=2,
∴-
×4=2,
解得k=-
经检验k=-
是方程的解.
由(1)知,当k=-
时,△<0,故原方程无实根
∴不存在符合条件的k的值.
| k |
| 4 |
解得k>-1,
又∵k≠0,
∴k的取值范围是k>-1且k≠0;
(2)不存在符合条件的实数k,
理由如下:
∵x1+x2=-
| k+2 |
| k |
| 1 |
| 4 |
又
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
∴-
| k+2 |
| k |
解得k=-
| 4 |
| 3 |
经检验k=-
| 4 |
| 3 |
由(1)知,当k=-
| 4 |
| 3 |
∴不存在符合条件的k的值.
点评:此题考查了根与系数的关系和一元二次方程的根的判别式,首先根据方程的判别式得到方程根的情况,然后将根与系数的关系与代数式变形相结合,得到所求字母的方程,解方程即可得到结果,但一定要注意此时k值一定要满足判别式>0.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
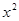 -kx-6=0的一个根为3,则实数k的值为(
)
-kx-6=0的一个根为3,则实数k的值为(
)