题目内容
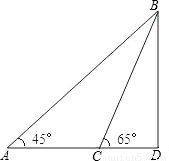
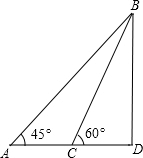 某海滨浴场的沿岸可以看作直线,如图所示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的D点,再跳入海中游到B点救助;若2号救生员从A跑到C,再跳入海中游到B点救助,且∠BCD=60°,且每位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.请你通过计算说明两位救生员谁先到达点B?
某海滨浴场的沿岸可以看作直线,如图所示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的D点,再跳入海中游到B点救助;若2号救生员从A跑到C,再跳入海中游到B点救助,且∠BCD=60°,且每位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.请你通过计算说明两位救生员谁先到达点B?分析:在Rt△ABD中求出AD、BD,可得出1号救生员所需时间,在Rt△BCD中,可求出CD从而求出2号救生员所需时间,从而比较两位救生员所用的时间即可作出判断.
解答:解:在Rt△ABD中,AD=BD=300米,
∵∠BCD=60°,
∴CD=
=100
米,BC=
=200
米,
则t1=
+
=200s,
t2=
+
≈194.3s,
∵200s>194.3s,
∴2号救生员先到.
∵∠BCD=60°,
∴CD=
| 300 |
| tan60° |
| 3 |
| 300 |
| sin60° |
| 3 |
则t1=
| 300 |
| 6 |
| 300 |
| 2 |
t2=
300-100
| ||
| 6 |
200
| ||
| 2 |
∵200s>194.3s,
∴2号救生员先到.
点评:本题考查了解直角三角形的应用,难度一般,熟练掌握解直角三角形的知识是解答本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
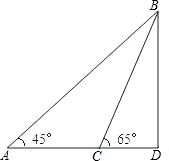 岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.
岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.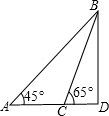 某海滨浴场的沿岸可以看作直线,如图示直线AD,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的D点,再跳入海中游到B点救助;若每位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.若2号救生员从A跑到C,再跳入海中游到B点救助,且∠BCD=65°,请问谁先到达点B?(所有数据精确到0.1,sin65°≈0.9,cos65°≈0.4,tan65°≈2,
某海滨浴场的沿岸可以看作直线,如图示直线AD,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的D点,再跳入海中游到B点救助;若每位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.若2号救生员从A跑到C,再跳入海中游到B点救助,且∠BCD=65°,请问谁先到达点B?(所有数据精确到0.1,sin65°≈0.9,cos65°≈0.4,tan65°≈2, 某海滨浴场的沿岸可以看作直线,如图示直线AD,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的D点,再跳入海中游到B点救助;若每位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.若2号救生员从A跑到C,再跳入海中游到B点救助,且∠BCD=65°,请问谁先到达点B?(所有数据精确到0.1,sin65°≈0.9,cos65°≈0.4,tan65°≈2,
某海滨浴场的沿岸可以看作直线,如图示直线AD,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的D点,再跳入海中游到B点救助;若每位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.若2号救生员从A跑到C,再跳入海中游到B点救助,且∠BCD=65°,请问谁先到达点B?(所有数据精确到0.1,sin65°≈0.9,cos65°≈0.4,tan65°≈2, ≈1.4)
≈1.4)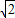 ≈1.4)
≈1.4)