题目内容
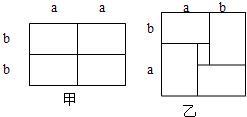
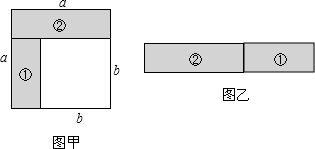
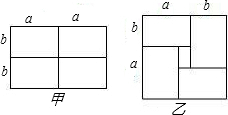
①如图甲所示是一个长为2a,宽为2b的长方形,若把此图沿图中虚线剪开均分为四块小长方形,然后按图乙的形状拼成一个正方形,请问:这两个图形的什么未改变________;用含a、b的式子表示:原长方形面积为________,正方形的面积为________正方形的面积比原长方形的面积多________.
②由①可得出下面的结论:在周长一定的长方形中,________时,此长方形的面积最大.
③若一长方形的周长为36cm,则当边长为多少时,该图形的面积最大?最大面积是多少?
周长 2a×2b (a+b)2 (a+b)2-4ab 边长相等
分析:根据长方形,正方形的周长,面积公式进行计算.长方形的周长公式2(a+b),正方形的周长公式:4a,长方形的面积公式:ab,正方形的面积公式a2.
解答:①原周长=2(2a+2b)=4a+4b.
变后的周长=4(a+b)=4a+4b.
∴周长未变.
原长方形面积=2a×2b=4ab.
正方形面积=(a+b)2.
∴正方形的面积-长方形的面积=(a+b)2-4ab=(a-b)2.
②当长与宽相等时,此长方形的面积最大.
③由②的结论可知,当长与宽相等时,此长方形的面积最大.
又∵长方形的周长为36cm.
∴当长=宽=9cm时,该长方形面积最大,最大面积为81cm2.
点评:此题主要考查了长方形的周长、面积公式的运用,熟记公式是解题的关键.
分析:根据长方形,正方形的周长,面积公式进行计算.长方形的周长公式2(a+b),正方形的周长公式:4a,长方形的面积公式:ab,正方形的面积公式a2.
解答:①原周长=2(2a+2b)=4a+4b.
变后的周长=4(a+b)=4a+4b.
∴周长未变.
原长方形面积=2a×2b=4ab.
正方形面积=(a+b)2.
∴正方形的面积-长方形的面积=(a+b)2-4ab=(a-b)2.
②当长与宽相等时,此长方形的面积最大.
③由②的结论可知,当长与宽相等时,此长方形的面积最大.
又∵长方形的周长为36cm.
∴当长=宽=9cm时,该长方形面积最大,最大面积为81cm2.

点评:此题主要考查了长方形的周长、面积公式的运用,熟记公式是解题的关键.

练习册系列答案
相关题目