题目内容
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF= ![]() .其中所有正确结论的个数是( )
.其中所有正确结论的个数是( ) 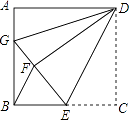
A.4
B.3
C.2
D.1
【答案】B
【解析】解:如图,由折叠可知,DF=DC=DA,∠DFE=∠C=90°, ∴∠DFG=∠A=90°,
在Rt△ADG和Rt△FDG中,![]() ,
,
∴Rt△ADG≌Rt△FDG,故①正确;
∵正方形边长是12,
∴BE=EC=EF=6,
设AG=FG=x,则EG=x+6,BG=12﹣x,
由勾股定理得:EG2=BE2+BG2 ,
即:(x+6)2=62+(12﹣x)2 ,
解得:x=4
∴AG=GF=4,BG=8,BG=2AG,故②正确;
BE=EF=6,△BEF是等腰三角形,易知△GED不是等腰三角形,故③错误;
S△GBE= ![]() ×6×8=24,S△BEF=
×6×8=24,S△BEF= ![]() S△GBE=
S△GBE= ![]() ×24=
×24= ![]() ,故④正确.
,故④正确.
综上可知正确的结论的是3个.
故选B.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目