题目内容
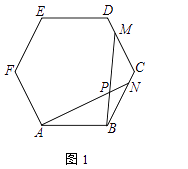
【题目】已知：△ABC内接于⊙O，连接AO并延长交BC于点D．
（1）如图1，求证；∠ABC+∠CAD=90°；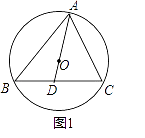
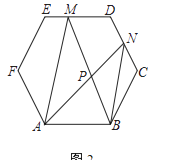
（2）如图2，过点D作DE⊥AB于E，若∠ADC=2∠ACB．求证：AC=2DE；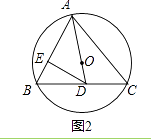
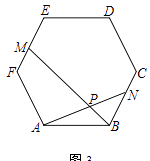
（3）如图3，在（2）的条件下，连接BO交DE于点F，延长ED交⊙O于点G，连接AG，若AC=6 
，BF=OD，求线段AG的长．
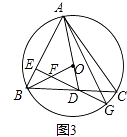
【答案】
（1）
证明：如图1中，延长AD交⊙O于点M，连接MC．
∵AM为⊙O的直径，
∴∠ACM=90°，
∴∠ABC=∠AMC，
∵∠AMC+∠MAC=90°，
∴∠B+∠CAD=90°．
（2）
证明：如图2中，过点O作OH⊥AC于H，连接BO．
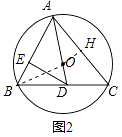
∴∠AOB=2∠ACB，
∵∠ADC=2∠ACB，
∴∠AOB=∠ADC，
∴∠BOD=∠BDO，
∴BD=BO，
∵∠BED=∠AHO，∠ABD=∠AOH，
∴△BDE≌△AOH，
∴DE=AH，
∵OH⊥AC，
∴AH=CH= 
AC，
∴AC=2DE．
（3）
证明：如图3中，过点O作ON⊥EG于N，OT⊥AB于T，连接OG．
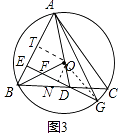
∵AC=6 
，AC=2DE，
∴DE=3 ，
∵OA=OB，
∴∠ABO=∠BAO，
∵∠ABO+∠BFE=90°，∠BAO+∠ADE=90°，
∴∠BFE=∠OFD=∠ODF，
∴OF=OD，
∵BF=OD，
∴OF=OD=BF，
∴△BFE≌△OFN，
∴BE=ON EF=FN
∵OF=OD，ON⊥FD，
∴EF=FN=ND= ，
∵BE=ON，OG=BD，
∴△BED≌△NOG，
∴ED=NG，
∴EG=5 ，
∵ON⊥EG OT⊥AB DE⊥AB，
∴四边形ONET为矩形，
∴BE=ET=ON，
∵OT⊥AB，
∴AT=BT，AE=3BE，
设AO=BD=r，OD= r，AD= 
r
在Rt△AED中，AE2=AD2﹣ED2，
在Rt△BED中，BE2=BD2﹣ED2，
即（ r）2﹣（3 ）2=9[（ r）2﹣（3 ）2]，
r=4 
或r=﹣4 （舍去），
∴AE=15，
在△AEG中，AG= 
=10 
．
【解析】（1）如图1中，延长AD交⊙O于点M，连接MC．首先证明∠ACM=90°，再证明∠ABC=∠M即可解决问题．（2）如图2中，过点O作OH⊥AC于H，连接BO．想办法证明△BDE≌△AOH即可解决问题．（3）如图3中，过点O作ON⊥EG于N，OT⊥AB于T，连接OG．由△BFE≌△OFN，推出BE=ON EF=FN由OF=OD，ON⊥FD，推出EF=FN=ND= ，由△BED≌△NOG，推出ED=NG，再证明AE=3BE，设AO=BD=r，OD= r，AD= r在Rt△AED中，AE2=AD2﹣ED2 ， 在Rt△BED中，BE2=BD2﹣ED2 ， 即（ r）2﹣（3 ）2=9[（ r）2﹣（3 ）2]，求出r即可解决问题．
