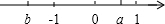题目内容
已知a、b、c在数轴上的位置如图所示，化简：|2a|-|a+c|-|1-b|+|-a-b|
∵a、c在原点的左侧，a＜-1，
∴a＜0，c＜0，
∴2a＜0，a+c＜0，
∵0＜b＜1，
∴1-b＞0，
∵a＜-1，
∴-a-b＞0
∴原式=-2a+（a+c）-（1-b）+（-a-b）
=-2a+a+c-1+b-a-b
=-2a+c-1．
故答案为：-2a+c-1．
∴a＜0，c＜0，
∴2a＜0，a+c＜0，
∵0＜b＜1，
∴1-b＞0，
∵a＜-1，
∴-a-b＞0
∴原式=-2a+（a+c）-（1-b）+（-a-b）
=-2a+a+c-1+b-a-b
=-2a+c-1．
故答案为：-2a+c-1．
练习册系列答案
相关题目
