题目内容
【题目】如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=6cm,求AD的长.

【答案】2
【解析】
根据等边对等角可得∠B=∠C,再利用三角形的内角和定理求出∠BAC=120°,然后求出∠CAD=30°,从而得到∠CAD=∠C,根据等角对等边可得AD=CD,再根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2AD,然后根据BC=BD+CD列出方程求解即可
∵AB=AC,
∴∠B=∠C=30°,
∴∠BAC=180°-2×30°=120°,
∵DA⊥BA,
∴∠BAD=90°,
∴∠CAD=120°-90°=30°,
∴∠CAD=∠C,
∴AD=CD,
在Rt△ABD中,
∵∠B=30°,∠BAD=90°,
∴BD=2AD,
∴BC=BD+CD=2AD+AD=3AD,
∵BC=6cm,
∴AD=2cm.

练习册系列答案
相关题目
【题目】甲、乙两名队员的10次射击训练,成绩分别被制成下列两个统计图.
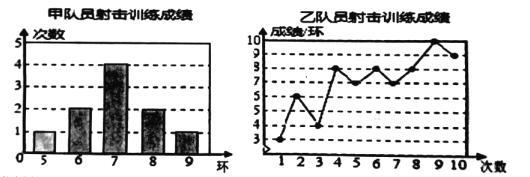
并整理分析数据如下表:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 |
|
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?