题目内容
如图，矩形的长和宽分别是4和3，等腰三角形的底和高分别是3和4，如果此三角形的底和矩形的宽重合，并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合．设矩形与等腰三角形重叠部分（阴影部分）的面积为y，重叠部分图形的高为x，那么y关于x的函数图象大致应为
A． | B． | C． | D． |
B
解析试题分析：如图，连接IE，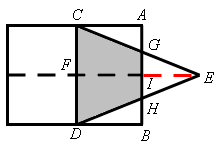
根据题意，CD=3，EF=4，FI=x，EI=4—x，
易得，△EGH∽△ECD，
∴
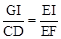，即
。∴
。
∴
。
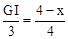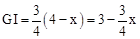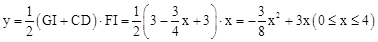∴y关于x的函数图象是抛物线在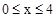
的一段，且当x=4时，y=6。
故选B。
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
函数
与
在同一坐标系中的大致图象是（ ）
A． | B． | C． | D． |
如图，抛物线
与双曲线
的交点A的横坐标是1，则关于
的不等式
的解集是（ ）
| A．x>1 | B．x<1 | C．0<x<1 | D．－1<x<0 |
直角坐标平面上将二次函数y=x2﹣2的图象向左平移1个单位，再向上平移1个单位，则其顶点为（ ）
| A．（0，0） | B．（1，﹣1） | C．（0，﹣1） | D．（﹣1，﹣1） |
若二次函数
(a≠0)的图象与x轴有两个交点，坐标分别为(x1，0)，(x2，0)，且x1<x2，图象上有一点M (x0，y0)在x轴下方，则下列判断正确的是
| A．a>0 | B．b2－4ac≥0 |
| C．x1<x0<x2 | D．a(x0－x1)( x0－x2)<0 |
数形结合是数学中常用的思想方法，试运用这一思想方法确定函数y=x2+1与
的交点的横坐标x0的取值范围是
| A．0＜x0＜1 | B．1＜x0＜2 | C．2＜x0＜3 | D．﹣1＜x0＜0 |
图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（
，y2）是抛物线上两点，则