题目内容
(2009•嘉定区一模)某条道路上通行车辆限速为80千米/小时,某校数学兴趣活动小组在距离道路60米的点P处建了一个监测点,并将道路上的AB段设定为监测区(如图),测得∠A=45°,∠B=30°,小轿车通过检测区的时间为6.5秒(精确到0.1秒,不考虑小轿车的车身长),请判断该轿车是否超速行驶简述解决问题的过程.(参考数据: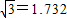 ).
).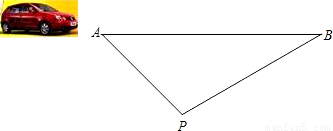
【答案】分析:过点P作PQ⊥AB,垂足为点Q,则PQ=60,可分别求出AQ、BQ的值,即可求出AB,从而求出小轿车通过检测区的速度,比较即可,注意统一单位.
解答: 解:过点P作PQ⊥AB,垂足为点Q,则PQ=60.(1分)
解:过点P作PQ⊥AB,垂足为点Q,则PQ=60.(1分)
在Rt△APQ中,∠A=45°.
∴AQ=60.(3分)
在Rt△BPQ中,∠B=30°, .
.
∴BQ=60×cot30°=60 .(3分)
.(3分)
∴AB=AQ+BQ=60+60 .(1分)
.(1分)
∵小轿车通过检测区的时间为6.5秒,80千米/小时≈22.2(米/秒);
小轿车通过检测区的速度为:(60+60 )÷6.5≈25.2(米/秒);(1分)
)÷6.5≈25.2(米/秒);(1分)
25.2(米/秒)>22.2(米/秒).
∴该轿车属于超速行驶.(1分)
点评:此题主要是运用所学的解直角三角形的知识解决实际生活中的问题.注意统一单位.
解答:
 解:过点P作PQ⊥AB,垂足为点Q,则PQ=60.(1分)
解:过点P作PQ⊥AB,垂足为点Q,则PQ=60.(1分)在Rt△APQ中,∠A=45°.
∴AQ=60.(3分)
在Rt△BPQ中,∠B=30°,
 .
.∴BQ=60×cot30°=60
 .(3分)
.(3分)∴AB=AQ+BQ=60+60
 .(1分)
.(1分)∵小轿车通过检测区的时间为6.5秒,80千米/小时≈22.2(米/秒);
小轿车通过检测区的速度为:(60+60
 )÷6.5≈25.2(米/秒);(1分)
)÷6.5≈25.2(米/秒);(1分)25.2(米/秒)>22.2(米/秒).
∴该轿车属于超速行驶.(1分)
点评:此题主要是运用所学的解直角三角形的知识解决实际生活中的问题.注意统一单位.

练习册系列答案
相关题目
 x2的图象向左平移1个单位,再向上平移3个单位,则所得图象的解析式为:
x2的图象向左平移1个单位,再向上平移3个单位,则所得图象的解析式为:  (x-1)2
(x-1)2 x2+3
x2+3 (x+1)2+3
(x+1)2+3 (x-1)2+3
(x-1)2+3
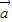 、
、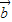 ,如图所示:
,如图所示: ,
,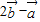 .
.