题目内容
【题目】如图,一次函数![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,函数
,函数![]() 与
与![]() 的图像交于第四象限的点
的图像交于第四象限的点![]() ,且点
,且点![]() 的横坐标为1.
的横坐标为1.
(1)求![]() 的值;
的值;
(2)观察图像,当![]() 满足 时,
满足 时,![]() ;
;
(3)在![]() 轴上有一点
轴上有一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交函数
轴的垂线,分别交函数![]() 和
和![]() 的图像于点
的图像于点![]() .若
.若![]() ,求
,求![]() 的值.
的值.

【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() 或
或![]()
【解析】
(1)先求出点C坐标,把点C的坐标代入函数![]() 即可求出
即可求出![]() 的值;
的值;
(2)观察图象,即可写出![]() 的取值范围.
的取值范围.
(3)把x=0代入y=x-3得y=-3,求出点B的坐标,根据![]() ,求出DE=9,D点坐标为(n,n-3),E点坐标为(n,-2n),列出方程即可解决问题.
,求出DE=9,D点坐标为(n,n-3),E点坐标为(n,-2n),列出方程即可解决问题.
解:(1)∵点C在直线![]() 的图象上,且点C的横坐标为1,
的图象上,且点C的横坐标为1,
∴点C的坐标为(1,![]() 2),
2),
把C(1,![]() 2)代入
2)代入![]() 得
得![]() 解得
解得![]() ;
;
(2)观察图象可知:
当![]() 时,
时,![]() ;
;
(3)把x=0代入y=x-3得y=-3,
∴B点坐标为(0,-3),即OB=3,
∵DE=3OB,
∴DE=9,
∵DE⊥x轴,P(n,0),
∴D点坐标为(n,n-3),E点坐标为(n,-2n)
∴![]()
∴n=4或n=-2.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
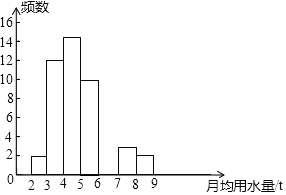
【题目】小明同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干居民的月均用水量(单位:t),并绘制了不完整的样本的频数分布表的频数分布直方图(如图)
根据上述图表回答下列问题:
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 0.04 |
3≤x<4 | 12 | 0.24 |
4≤x<5 | ||
5≤x<6 | 10 | 0.2 |
6≤x<7 | 0.12 | |
7≤x<8 | 3 | 0.06 |
8≤x<9 | 2 | 0.04 |
(1)小明同学共调查了多少户居民的月均用水量;
(2)请根据题中已有的信息补全频数分布表和频数分布直方图;
(3)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的等用水量家庭大约有多少户?