题目内容
【题目】如图,直线AB与CD相交于点O,∠AOM=90°. 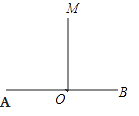
(1)如图1,若OC平分∠AOM,求∠AOD的度数 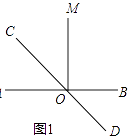
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数. 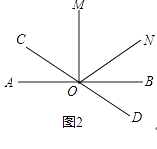
【答案】
(1)解:∵∠AOM=90°,OC平分∠AOM,
∴∠AOC= ![]() ∠AOM=
∠AOM= ![]() ×90°=45°,
×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°﹣∠AOC=180°﹣45°=135°,
即∠AOD的度数为135°
(2)解:∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB﹣∠BON=4x°﹣x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON= ![]() ∠CON=
∠CON= ![]() x°,
x°,
∵∠BOM= ![]() x+x=90°,
x+x=90°,
∴x=36°,
∴∠MON= ![]() x°=
x°= ![]() ×36°=54°,
×36°=54°,
即∠MON的度数为54°
【解析】(1)根据角平分线的定义求出∠AOC=45°,然后根据邻补角的定义求解即可;(2)设∠NOB=x°,∠BOC=4x°,根据角平分线的定义表示出∠COM=∠MON= ![]() ∠CON,再根据∠BOM列出方程求解x,然后求解即可.
∠CON,再根据∠BOM列出方程求解x,然后求解即可.
【考点精析】本题主要考查了角的平分线和对顶角和邻补角的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个才能正确解答此题.

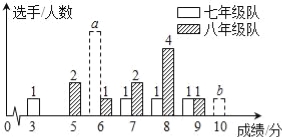
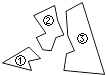
【题目】2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m= ,n= ;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.