题目内容
【题目】如图,已知A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1 , y1)平移后的对应点为P′(x1+6,y1+4). 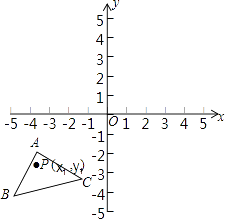
(1)请在图中作出△A′B′C′;
(2)写出点A′、B′、C′的坐标.
【答案】
(1)解:∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),
∴平移规律为:向右平移6个单位,向上平移4个单.
如图所示:
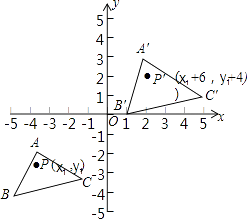
(2)解:A′(2,3),B′(1,0),C′(5,1)
【解析】(1)由点P(x1 , y1)平移后的对应点为P′(x1+6,y1+4)可得其平移规律为:向右平移6个单位,向上平移4个单位;故把△ABC的各顶点向右平移6个单位,再向上平移4个单位,顺次连接各顶点即为△A′B′C′;(2)根据各点所在的象限和距离坐标轴的距离得到平移后相应各点的坐标即可.

练习册系列答案
相关题目
【题目】某山区有23名中小学生因贫困失学需要捐助,资助一名中学生需要学习费用a元,资助一名小学生需要学习费用b元,某校学生积极捐款,初中各年级学生捐款数额与用其恰好能帮助的贫困中学生和小学生人数的部分情况如下表:
七年级 | 八年级 | 九年级 | |
捐款数额(元) | 4000 | 4200 | 7400 |
捐助贫困中学生(名) | 2 | 3 | |
捐助贫困小学生(名) | 4 | 3 |
(1)求a、b的值;
(2)九年级学生的捐款解决了其余贫困中小学生的学习费用,请将九年级学生可捐助的贫困中、小学生人数直接填入上表中(不需要写出计算过程).