题目内容
(2012•建宁县质检)如图:在直角坐标系中,以点A(3,0)为圆心,以5为半径的圆与x轴相交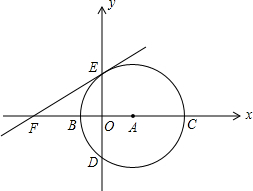 于B、C两点,与y轴相交于D、E两点.
于B、C两点,与y轴相交于D、E两点.
(1)若抛物线y=
x2+bx+c经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?
(2)过点E的直线y=kx+m交x轴于F(-
,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;
(3)探索:是否能在(1)中的抛物线上找到一点Q,使直线BQ与x轴正方向所夹锐角的正切值等于
?若能,请直接写出Q点坐标;若不能,请说明理由.
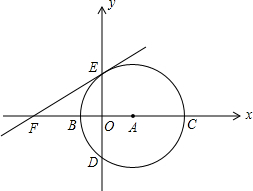 于B、C两点,与y轴相交于D、E两点.
于B、C两点,与y轴相交于D、E两点.(1)若抛物线y=
| 1 |
| 4 |
(2)过点E的直线y=kx+m交x轴于F(-
| 16 |
| 3 |
(3)探索:是否能在(1)中的抛物线上找到一点Q,使直线BQ与x轴正方向所夹锐角的正切值等于
| 1 |
| 4 |
分析:(1)连接AE,利用垂径定理可求出点D的坐标为(0,-4),根据圆的半径为5,可得出点C的坐标为(8,0),利用待定系数法求解即可;
(2)根据直线经过点E(0,4),可设直线解析式为y=kx+4,将点F的坐标代入可得出直线解析式,分别求出EF2,AF2,AE2,利用勾股定理的逆定理判断出∠AEF为直角,继而根据切线的判定可得出结论;
(3)由(1)得点B在抛物线上,设点Q的坐标为(x,
x2-
x-4),分别讨论点Q的位置,①点Q在x轴上方,②点Q在x轴下方,利用正切值建立方程,解出即可得出答案.
(2)根据直线经过点E(0,4),可设直线解析式为y=kx+4,将点F的坐标代入可得出直线解析式,分别求出EF2,AF2,AE2,利用勾股定理的逆定理判断出∠AEF为直角,继而根据切线的判定可得出结论;
(3)由(1)得点B在抛物线上,设点Q的坐标为(x,
| 1 |
| 4 |
| 3 |
| 2 |
解答:解:连接AE,
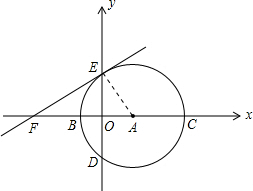
由题意得,OD=OE=4,
故可得:C、D两点坐标为:C(8,0),D(0,-4),
把C、D两点坐标代入y=
x2+bx+c中,
得:
,
解得:b=-
,
故所求二次函数为:y=
x2-
x-4,
∵B点坐标为(-2,0),
∴当x=-2时,y=
×(-2)2-
×(-2)-4=0,
∴点B在这条抛物线上.
(2)因为直线经过点E(0,4),可设解析式为:y=kx+4,
把点F(-
,0)代入上式得:k=
,
故所求一次函数为:y=
x+4,
在Rt△OEF中,EF2=OE2+OF2=16+
=
,
在△AEF中,AF=3+
=
,
即AF2=
,
∴EF2+AE2=
+25=
=AF2,
∴∠AEF=90°,
∴EF是⊙O的切线.
(3)能找到这样的点Q,
设存在点Q(x,
x2-
x-4),
∵直线BQ与x轴正方向所夹锐角的正切值等于
,
①若点Q在x轴上方时,此时
=
,
解得:x1=9,x2=-2(舍去),
故此时点Q的坐标为(9,
);
②若点Q在x轴下方时,
=
,
解得:x1=7,x2=-2(舍去),
故此时点Q的坐标为(7,-
).
故可得存在点Q的坐标,其坐标分别为:(9,
) 和 (7,-
).
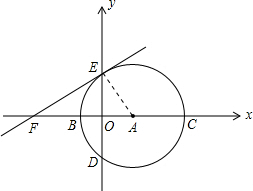
由题意得,OD=OE=4,
故可得:C、D两点坐标为:C(8,0),D(0,-4),
把C、D两点坐标代入y=
| 1 |
| 4 |
得:
|
解得:b=-
| 3 |
| 2 |
故所求二次函数为:y=
| 1 |
| 4 |
| 3 |
| 2 |
∵B点坐标为(-2,0),
∴当x=-2时,y=
| 1 |
| 4 |
| 3 |
| 2 |
∴点B在这条抛物线上.
(2)因为直线经过点E(0,4),可设解析式为:y=kx+4,
把点F(-
| 16 |
| 3 |
| 3 |
| 4 |
故所求一次函数为:y=
| 3 |
| 4 |
在Rt△OEF中,EF2=OE2+OF2=16+
| 256 |
| 9 |
| 400 |
| 9 |
在△AEF中,AF=3+
| 16 |
| 3 |
| 25 |
| 3 |
即AF2=
| 625 |
| 9 |
∴EF2+AE2=
| 400 |
| 9 |
| 625 |
| 9 |
∴∠AEF=90°,
∴EF是⊙O的切线.
(3)能找到这样的点Q,
设存在点Q(x,
| 1 |
| 4 |
| 3 |
| 2 |
∵直线BQ与x轴正方向所夹锐角的正切值等于
| 1 |
| 4 |
①若点Q在x轴上方时,此时
| ||||
| x-(-2) |
| 1 |
| 4 |
解得:x1=9,x2=-2(舍去),
故此时点Q的坐标为(9,
| 11 |
| 4 |
②若点Q在x轴下方时,
-(
| ||||
| x-(-2) |
| 1 |
| 4 |
解得:x1=7,x2=-2(舍去),
故此时点Q的坐标为(7,-
| 9 |
| 4 |
故可得存在点Q的坐标,其坐标分别为:(9,
| 11 |
| 4 |
| 9 |
| 4 |
点评:此题属于圆的综合题,涉及了切线的判定、待定系数法求函数解析式及三角函数的知识,综合性较强,难度较大,解答本题的关键是掌握各个知识点之间的融会贯通.

练习册系列答案
相关题目

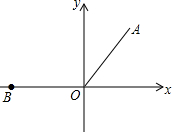 (2012•建宁县质检)如图:在直角坐标系中,线段OA=6cm,OA与y轴的夹角为30°.将线段OA绕原点按逆时针方向旋转到x轴的负半轴上,得到线段OB.
(2012•建宁县质检)如图:在直角坐标系中,线段OA=6cm,OA与y轴的夹角为30°.将线段OA绕原点按逆时针方向旋转到x轴的负半轴上,得到线段OB.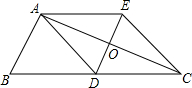 (2012•建宁县质检)如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.
(2012•建宁县质检)如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.